2-modulusdeler
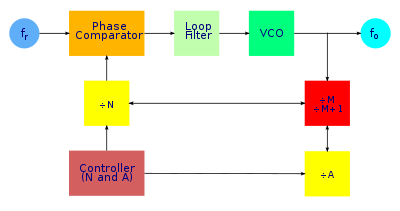
* Højre gule kasses nederste input-signal kommer fra datalinjen mellem venstre gul kasse og højre røde, det kan ikke ses direkte af tegningen.[1]
* 2-modulusdeler udgøres af højre røde kasse.
* Brun kasse er delevalg som bestemmes af brugeren typisk med drejeknapper eller kontakter via logikkredsløb som f.eks. en mikrocontroller.

Indenfor den digitale elektronik bruges betegnelsen modulus om en delers deletal, det vil sige det antal pulser der skal til for at udgangen gennemløber en periode.
En 2-modulsdeler kan sættes til 2 forskellige deletal, alt efter om styreterminalen er høj eller lav. Den sidder i forbindelse med programmerbare delere og giver sammen med dem muligheden for at kunne skabe en deler med et vilkårligt deletal, ofte brugt i frekvenssynteser, hvor en enkelt krystaloscillator via et faselåst kredsløb giver mulighed for at skifte mellem alle radiokanaler i et vist frekvensbånd.
De 2 modulus bestemmes af kanalafstanden, referencefrekvensen og resten af delerens konstruktion, og kan f.eks. være 10 og 11 (en 10/11-deler) eller 40 og 41.
Problemet[redigér | rediger kildetekst]
En frekvenssyntese producerer en variabel output frekvens, fo, dannet via det faselåste kredsløbs referencefrekvens, fr og hvor det variable heltal (deletal) N er deletallet for en tæller:
Hvis man ønsker at lave f.eks. fo=150,025MHz og fr=25kHz skal:
Men har man anvendt en fast fordeler (eng. prescaler) på f.eks. 16, skal N=6001/16=375,0625 hvilket ikke er et heltal.
Én løsning er at sænke fr sænkes til 25kHz/16 for at alle nye N kan blive heltallige. Der er en stor ulempe ved at sænke fr til så lav en frekvens og det er at det faselåste kredsløb så bliver længere tid om at låse.
Løsningen[redigér | rediger kildetekst]
Løsningen er at anvende en 2-modulusdeler og to delere kaldet A og N – i stedet for den ene N.
Deler A skal være strengt mindre end A end deler N. Begge delere bliver clocket af 2-modulusdelerens output, men kun deler N's output sendes tilbage til fasekomparatoren.
Løkke:
- Initielt sættes 2-modulusdeleren til at dele med M + 1. Både N og A tæller ned indtil A når nul og så skiftes 2-modulusdeleren til at dele med M. På dette punkt, har deleren N talt A. Tællingen fortsætter indtil N når nul, hvilket er yderligere N - A tællinger. På dette punkt fortsætter cyklussen.
Formler:
Så mens vi stadig har en faktor M som multipliceres med N, kan vi yderligere lægge en tælling på A til, hvilket giver en deler med en brøkdel. Kun 2-modulusdeleren behøver at blive konstrueret af højhastighedslogik, og referencefrekvensen kan blive på den ønskede output-frekvensafstand.
A og N kan beregnes med følgende formler:
hvor V er det kombinerede divisionsforhold V = MN+A. For at dette virker efter hensigten, skal A være strengt mindre end M, såvel som mindre end eller lig N. Disse restriktioner på værdier af A medfører at du ikke kan få ethvert divisionsforhold V. Hvis V falder under M(M - 1), vil nogle kanaler mangle.
Kilder/referencer[redigér | rediger kildetekst]
Eksterne henvisninger[redigér | rediger kildetekst]
- Fra side 24: PLL Performance, Simulation, and Design 4th Edition. Dean Banerjee Arkiveret 7. juni 2011 hos Wayback Machine



![{\displaystyle {\begin{aligned}&f_{o}=f_{r}\left[{M(N-A)+(M+1)A}\right]\\\Rightarrow &f_{o}=f_{r}\left(MN+A\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/578792c2d2913f526565be397918f68005a87836)
