Moskva-papyrussen

Moskva-papyrussen eller Papyrus Moskva 4676 er en papyrusrulle om egyptisk matematik. Den kaldes også Golenishchev Matematik Papyrus efter rullens første ejer uden for Egypten, ægyptologen Vladimir Golenisjtjov. Golenisjtjov købte papyrussen i 1892 eller 1893 i Theben. Senere kom den ind i Pusjkinmuseets samling i Moskva, hvor den findes i dag.
Baseret på palæografi og ortografi i den hieratiske tekst blev den sandsynligvis nedskrevet under det 13. dynasti og er baseret på ældre materiale, som givetvis stammer fra det 12. egyptiske dynasti, omkring 1850 f.v.t.[1] Papyrussen er omkring 5½ m lang og mellem 3,8 og 7,6 cm bred. Den blev delt op i 25 problemer med løsninger af den sovjetiske orientalist Vasilij Vasilijevitj Struve[2] i 1930.[3] Sammen med Rhind-papyrussen er den blandt de berømte papyrusser, og disse to ruller er hovedkilder til ægypternes matematik.[4] Moskva-papyrussen er ældre end Rhind-papyrussen, mens sidstnævnte er den største.[5]
Opgaver i Moskvapapyrussen[redigér | rediger kildetekst]
Problemerne i Moskva-papyrussen følger ikke nogen speciel orden, og løsningerne af problemerne er langt mindre detaljerede end dem, der findes i Rhind-papyrussen- Papyrusrullen er særlig kendt for geometriske problemer. Problem 10 og 14 beregner henholdsvis overfladearealet og volumen af en keglestub. De resterende problemer er af mere almindelig natur.[1]
Shipes delingsproblemer[redigér | rediger kildetekst]
Problem 2 og 3 handler om opdeling af et skib. Et problem beregner længden af et skibs ror og det andet beregner længden af et skibs mast, givet at den er 1/3 + 1/5 af længden på en cedertræsstamme der er 30 cubit lang.[1]
Aha-problemer[redigér | rediger kildetekst]
| Aha skrevet med hieroglyffer | |||
|
Aha-problemerne er at finde ukendte kvantiteter (refereret til som Aha), hvis en del af kvantiteten og dele af den er givet. Rhind-papyrussen indeholder også fire af disse problemer. Problem 1, 19 og 25 på Moskva-papyrussen er Aha-problemer. Eksempelvis er problem 19 at beregne antallet, når man har 1 og ½ gange og lægger 4 til for at få 4.[1] I new math går opgaven ud på at løse
Pefsu-problemer[redigér | rediger kildetekst]
De fleste af problemerne er pefsu problemer: 10 af de 25 problemer er af denne type. En pefsu måler styrken på en øl lavet fra en heqat af korn
Et højere pefsu-nummer betyder svagere brød eller øl. Pefsu-tallet bliver nævnt på mange offerlister. Eksempelvis oversættes problem 8 til:
- (1) Eksempel på at beregne 100 stykker brød af pefsu 20
- (2) Hvis nogen siger til dig: "Du har 100 skiver brød af 20 pefsu
- (3) som skal byttes med øl af pefsu 4
- (4) lige 1/2 1/4 malt-øl"
- (5) Først beregnes det korn, der skal bruges til at lave 100 skiver brød af pefsu 20
- (6) Resultatet er 5 heqat. Derefter udregner du, hvad du skal bruge for en des-kande med øl, ligesom øllen kaldet 1/2 1/4 maltøl
- (7) Resultatet er 1/2 af den målte heqat skal bruges til en des-kande med øl lavet med korn fra det Øvre Egypten.
- (8) Beregn 1/2 af 5 heqat, resultat vil være 2 1/2
- (9) Tag disse 2 1/2 fire gange
- (10) Resultatet er 10. Så siger du til ham:
- (11) "Se! Mængden af øl findes at være korrekt."[1]
Baku-problemer[redigér | rediger kildetekst]
Problem 11 og 23 er Baku-problemer. De beregner arbejderes produktion. Problem 11 spørger: hvis én bringer 100 stammer, der måler 5 × 5, hvor mange stammer der måler 4×4 svarer det til? Problem 23 beregner, hvor meget en skomager kan lave ved at han skærer og dekorerer sandaler.[1]
Geometriproblemer[redigér | rediger kildetekst]
Syv af de 25 problemer omhandler geometri og går fra at beregnes arealet af trekanter til at finde overfladen på en halvkugle (problem 10) og at finde volumenet af en keglestub eller pyramidestub.[1]
To interessante geometriske problemer[redigér | rediger kildetekst]
Problem 10[redigér | rediger kildetekst]
Det tiende problem i Moskva-papyrussen spørger om at overfladen på en halvkugle skal beregnes (Struve, Gillings) eller muligvis af en semi-cylinder (Peet). Nedenfor antages at beregningerne omhandler en halvkugle.
Teksten lyder: "Eksempel på at beregnet en kurv. Du får en kurv med en åbning på 4 1/2. Hvad er overfladen? Tag 1/9 af 9 (da) kurven er en halv æggeskal. Du får 1. Beregner resten, hvilket er 8. Beregn 1/9 af 8. Du får 2/3 + 1/6 + 1/18. Find ud af hvad resten af disse 8 er efter at fratrække 2/3 + 1/6 + 1/18. Du får 7 + 1/9. Multiplicer 7 + 1/9 med 4 + 1/2. Du får 32. Se dette er dens overflade. Du har fundet det korrekt."[1][6]
Løsningen svarer til at beregne er areal som
Dette betyder at teksten i Moskva-papyrussen brug til at approksimere pi].
Problem 14: Volumen af en kvadratisk pyramidestub[redigér | rediger kildetekst]
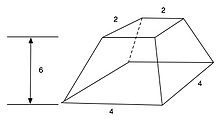
Det fjortende problem i Moskva-papyrussen beregner volumen af en pyramidestub. Den går også under navnet "Den største ægyptiske pyramide".[7]
Problem 14 skriver, at en pyramide er forkortet, så toppen et kvadrat med enhedslængden 2, og bunden er et kvadrat med enhedslængden 4, og højden er 4. Volumen findes at være 56 kubikenheden, hvilket er korrekt.[1]
Teksten lyder: "Hvis du får at vide: 6 høj og grundfladen har 4, mens topstykket har 2, så skal du kvadrere de 4. Det bliver 16; du skal gange de 2 med 4, det er 8; du skal kvadrere de 2, det er 4. Nu skal du lægge 16, 8 og 4 sammen, det er 28. Nu skal du tage en tredjedel af de 6. Det er 2. Du skal gange de 28 med de 2, resultatet er 56. Det er sandelig rumfanget af pyramidestubbet!"[7][8]
Løsningen på problemet indikerer at egypterne kendte til den rigtige formel til at beregne volumen af en pyramidestub:
Forskere har spekuleret på, hvordan egypterne har fundet frem til formlen for volumen på en keglestub, men udledningen af formlen bliver ikke beskrevet i papyrussen.[9]
Andre papyrus[redigér | rediger kildetekst]
Generellse papyrusruller:
Referencer[redigér | rediger kildetekst]
- ^ a b c d e f g h i Clagett, Marshall. 1999. Ancient Egyptian Science: A Source Book. Volume 3: Ancient Egyptian Mathematics. Memoirs of the American Philosophical Society 232. Philadelphia: American Philosophical Society. ISBN 0-87169-232-5
- ^ "Struve V.V., (1889–1965), orientalist :: ENCYCLOPAEDIA OF SAINT PETERSBURG". Arkiveret fra originalen 13. februar 2012. Hentet 23. august 2016.
- ^ Struve, Vasilij Vasil'evič, and Boris Turaev. 1930. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau. Quellen und Studien zur Geschichte der Mathematik; Abteilung A: Quellen 1. Berlin: J. Springer
- ^ Matematik i oldtiden Arkiveret 17. september 2016 hos Wayback Machine. ice-j.dk. Hentet 23/8-2016
- ^ Great Soviet Encyclopedia, 3rd edition, entry on "Папирусы математические", available online here Arkiveret 26. marts 2020 hos Wayback Machine
- ^ Williams, Scott W. Egyptian Mathematical Papyri
- ^ a b Matematikundervisninger omkring år 1800 f.v.t.. Københavns Universitet. Hentet 23/8-2016
- ^ som beskrevet i Gunn & Peet, Journal of Egyptian Archaeology, 1929, 15: 176. Se også, Van der Waerden, 1961, Plate 5
- ^ Gillings, R. J. (1964), "The volume of a truncated pyramid in ancient Egyptian papyri", The Mathematics Teacher, 57 (8): 552-555, JSTOR 27957144,
While it has been generally accepted that the Egyptians were well acquainted with the formula for the volume of the complete square pyramid, it has not been easy to establish how they were able to deduce the formula for the truncated pyramid, with the mathematics at their disposal, in its most elegant and far from obvious form
.
Fuld tekst af Moskva-papyrussen[redigér | rediger kildetekst]
- Struve, Vasilij Vasil'evič, og Boris Turaev. 1930. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau. Quellen und Studien zur Geschichte der Mathematik; Abteilung A: Quellen 1. Berlin: J. Springer
Andre referencer[redigér | rediger kildetekst]
- Allen, Don. April 2001. The Moscow Papyrus Arkiveret 27. marts 2018 hos Wayback Machine and Summary of Egyptian Mathematics Arkiveret 27. maj 2001 hos Wayback Machine.
- Imhausen, A., Ägyptische Algorithmen. Eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten, Wiesbaden 2003.
- Mathpages.com. The Prismoidal Formula.
- O'Connor and Robertson, 2000. Mathematics in Egyptian Papyri.
- Truman State University, Math and Computer Science Division. Mathematics and the Liberal Arts: Ancient Egypt and The Moscow Mathematical Papyrus.
- Williams, Scott W. Mathematicians of the African Diaspora, containing a page on Egyptian Mathematics Papyri.
- Zahrt, Kim R. W. Thoughts on Ancient Egyptian Mathematics Arkiveret 27. september 2011 hos Wayback Machine.





