Funktion (matematik)

Sammenskrivningsforslag Artiklerne Afbildning (matematik), Funktion (matematik) er foreslået sammenskrevet.  Diskutér forslaget

Eksempel på et lille udsnit af funktionen eller afbildningen med parameteren x: y = x³, x tilhører R.

Inden for matematikken er en funktion et redskab der beskriver hvordan en såkaldt afhængig variabel størrelse varierer som en konsekvens af ændringer i en anden, såkaldt uafhængig variabel. Kalder man den uafhængige variabel for x og den afhængige for y, skrives en funktion helt kort som

y = f(x)

Denne notation blev første gang brugt af matematikeren Leonhard Euler. Bogstavet f skal blot betragtes som et »navn«, ligesom x er et »navn« der dækker over et tal. Et grundlæggende træk ved funktioner er, at der til en bestemt værdi af x hører én og kun én værdi af y.

Man kan tænke sig en funktion som en art maskine, der som »råmateriale« tager imod et tal (den uafhægige variabel), og til gengæld afleverer et andet tal (den afhængige variabel). Har man én gang konstateret at maskinen afleverer et 5-tal hvis man fodrer den med et 2-tal, kan man være sikker på at få »5« ud hver eneste gang man putter »2« ind i den.

Funktioner som sammenknytning af mængder

En funktion er en "sammenknytning" af elementer mellem to mængder. Der er mere præcist tale om en funktion (fx benævnt $f$) fra en mængde A til en mængde B, hvis der for alle $a\in A$ er knyttet ét element $b\in B$. Dette skrives som $f:A\rightarrow B$.

Mængden A kaldes funktionens domæne eller definitionsmængde, mens mængden B kaldes codomænet eller dispositionsmængden.

Sammenknytning mellem konkrete elementer skrives som $f(a)=b$ og kan bruges til at definere selve funktionen. Hvis eksempelvis $A=\{\Box ,\triangle ,\Diamond \}$ og $B=\{\clubsuit ,\heartsuit \}$, så kunne funktionen $f:A\rightarrow B$ eksempelvis være givet ved: $f(\Box )=\heartsuit ,f(\triangle )=\clubsuit ,f(\Diamond )=\heartsuit$.

Ordet afbildning anvendes ofte synonymt med funktion.

Er A og B i stedet talmængder, kan man definere funktionen ved hjælp af regneudtryk, hvilket der gives talrige eksempler på i det følgende.

Forskrift

Den nøjere sammenhæng mellem den uafhængige og afhængige variabel kan være givet ved et regneudtryk der beregner hvad den afhængige variabel bliver for en given værdi af den uafhængige. I ovenstående analogi kan man samnenligne denne forskrift med den »indmad" i maskinen, som sørger for at danne det tal der kommer ud af maskinen. Forskriften i eksemplet med maskinen kunne f.eks. se sådan her ud:
f(x) = 2·x + 1

Definitions- og værdimængde

I forbindelse med en given funktion f findes der to mængder med særlig relevans: Definitionsmængden til f, der ofte skrives som Dm(f), og værdimængden til f, der ofte skrives som Vm(f). Funktionen f siges at være "defineret på mængden Dm(f)".

Definitionsmængden er populært sagt mængden af tal som den uafhængige variabel x må være lig med. I forbindelse med føromtalte maskine kan man forestille sig definitionsmængden som en kasse indeholdende alle de tal som maskinen kan behandle. Stiller man en tom kasse op der hvor maskinen spytter tal ud, og sender alle tallene i definitionsmængde-kassen igennem, ender den nye kasse med at indeholde alle de værdier som den afhængige variabel kan antage: Mængden af disse tal kaldes for værdimængden til funktionen f.

Med en forskrift som f(x) = 2·x + 1 kunne definitionsmængden f.eks. være mængden af reelle tal $\mathbb {R}$. I så fald vil værdimængden også være de reelle tal. I andre situationer lader funktionsværdien sig kun beregne for visse værdier af x, f.eks.:

g(x) = ln x - 1

Ønsker man at værdimængden kun skal indeholde reelle tal, sætter det begrænsninger på definitionsmængden. Eftersom ln x (den naturlige logaritme til x; i sig selv en funktion) kun er reel for positive, reelle x, kan regneudtrykket kun beregnes for sådanne værdier, og definitionsmængden til g bliver da $\mathbb {R} _{+}$; mængden af positive reelle tal. Alternativt kunne definitionsmængden f.eks. vælges til at være alle reelle tal; værdimængden bliver så en delmængde af de komplekse tal.

Hvis funktionen bruges som model af praktiske forhold, kan sammenhængen tilsige andre begrænsninger i definitionsmængden. Hvis x eksempelvis beskriver hvor mange 6'ere man har fået ved at kaste en terning, må x næsten nødvendigvis være et ikke-negativt heltal, eftersom et »halvt antal seksere« ikke giver megen mening i denne sammenhæng.

Monotoni

Visse funktioner, som eksemplet med f(x) = 2·x + 1, har den egenskab, at hvis den uafhængige variabel x stiger en lille smule, vil det afhængige y også stige: Sådan en funktion siges at være monotont voksende - monotont eftersom den aldrig »gør andet« end at stige, uanset hvilken værdi af x man går ud fra.
Med andre funktioner, f.eks. y = g(x) = 1/x vil y konsekvent falde hvis man forøger x en kende: Sådanne funktioner omtaler matematikerne tilsvarende som monotont aftagende. Atter andre funktioner, som f.eks. sinus og cosinus er voksende indenfor bestemte intervaller for x, og aftagende når x falder imellem disse intervaller.
Oplysninger om i hvilke intervaller en given funktion er hhv. voksende og aftagende kaldes almindeligvis for funktionens monotoniforhold.

Invers funktion

Hvis en funktion f(x) enten har samme monotoni (enten voksende eller aftagende) i hele sin definitionsmængde, findes der en såkaldt invers funktion til den pågældende funktion, som skrives f ^-1(x): Denne inverse funktion kan tage imod et tal der er beregnet med f(x), og så at sige "regne baglæns" for at finde tilbage til x: Hvis f(3) = 12, så vil f ^-1(12) være lig med 3 eller hvis f(x)=x² så er f ^-1(x)=√x
Heraf ses, at det der er definitionsmængden til f, bliver værdimængden til f ^-1, mens værdimængden af f er f ^-1's definitionsmængde. Altså:
Dm(f) = Vm(f ^-1), og Vm(f) = Dm(f ^-1).

Hvis en funktion ikke har samme monotoni i hele sin definitionsmængde, f.eks. sinus, kan man i "streng" matematisk forstand ikke uden videre indføre dens inverse funktion, fordi én værdi af x vil kunne give mere end én funktionsværdi. Men da det er praktisk at kunne "regne baglæns" og finde det x der giver en vis værdi af sin(x), har man alligevel indført den inverse funktion sin ^-1(x). Hvis man afgrænser definitionsmængden til sinus-funktionen til intervallet indenfor ±90° eller ±π/2 radianer, er sinus monotont voksende, og for sinus i dette interval kan man således tale om en invers funktion.

Se også sammensat funktion.

Regning med funktioner

Når f og g er funktioner med samme definitionsmængde (hvis definitionsmængderne er forskellige, kan man restringere til deres fællesmængde) kan man, hvis de to funktioner tager værdier i de komplekse tal, indføre nye funktioner f+g, f-g, f·g og f/g ved punktvise operationer. Det vil sige at de nye funktioner er defineret ved

• (f+g)(x) = f(x) + g(x)
• (f-g)(x) = f(x) - g(x)
• (f·g)(x) = f(x)·g(x)
• (f/g)(x) = f(x)/g(x)

idet den sidste funktion kun er veldefineret hvor g(x)$\neq$0.

Særlig agtpågivenhed må udvises når skrivemåder som f³ anvendes, altså potenser af en funktion. Notationen kan nemlig fortolkes på to måder: enten som punktvis multiplikation (som ovenfor) eller som funktionssammensætning (se dette). Eksplicit kan f³ betyde

• $f^{3}(x)=(f\cdot f\cdot f)(x)=f(x)\cdot f(x)\cdot f(x)=(f(x))^{3}$

eller

• $f^{3}(x)=(f\circ f\circ f)(x)=f(f(f(x)))$

Hvilken betydning der er relevant, må forstås af sammenhængen.

Almene polynomier

Forskriften for en ret linje, eller et 1.gradspolynomium, er givet ved

$f(x)=a\cdot x+b$

Forskriften for en parabel, eller et 2.gradspolynomium, er givet ved:

$f(x)=a\cdot x^{2}+b\cdot x+c$

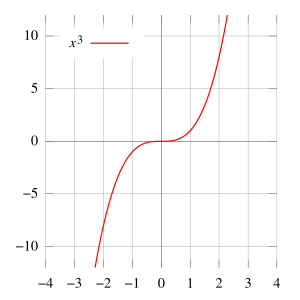
Forskriften for en 3.gradsfunktion / 3.gradspolynomium er givet ved:

$f(x)=a\cdot x^{3}+b\cdot x^{2}+c\cdot x+d$

Potentielle funktioner

Forskriften for en potentiel funktion er givet ved:

$f(x)=b\cdot x^{a},\ \ x>0$

Hvor "b" bestemmer væksthastigheden sammen med "a".

Man kan undersøge om en sammenhæng er en potensfunktion ved at tegne den på dobbeltlogaritmisk papir og se om man får en ret linje

Potensfunktioner

Forskriften for en potensfunktion er givet ved:

$f(x)=x^{a},\ \ x>0$

En potensfunktion kan, i lighed med en potentiel funktion indtegnes på dobbeltlogaritmisk papir hvor det vil give en ret linje.

Eksponentialfunktioner

Forskriften for en eksponentialfunktion er givet ved:

$f(x)=b\cdot a^{x}$

Hvor "b" er skæring med y-aksen og "a" er udviklingens hastighed. Hvis a<1 er grafen aftagende, hvis a=1 fremkommer en vandret linje, og hvis a>1 vil grafen være voksende.

En anden meget kendt eksponentialfunktion er:

$f(x)=e^{x},\ \ e=2.718281828...$

Man kan undersøge om en funktion er en eksponentialfunktion ved at indtegne funktionen på enkeltlogaritmisk papir. Hvis det giver en ret linje er det en eksponentialfunktion.

Logaritmiske funktioner

Logaritmiske funktioner er den omvendte funktion af en eksponentialfunktion, dvs. y-værdierne føres over i x-værdierne. Her er to eksempler på logaritmiske funktioner:

$f(x)=\ln x,\ \ x>0,\ \ a=e$

$f(x)=\log x,\ \ x>0,\ \ a=10$

Hvor a henviser til hvilken eksponentialfunktion der er tale om, også kaldet grundtallet. I matematik beteger e som oftest Eulers tal.

Trigonometriske funktioner

De tre almindelige trigonometriske funktioner er givet ved:

$f(x)=\sin x\,\!$
$f(x)=\cos x\,\!$

$f(x)=\tan x\,\!$

f(x)=sin(x) bruges bl.a. i fysik til at beskrive hvordan strøm og bølger bevæger sig inden for et bestemt tidsrum. Desuden har funktioner for sinus og cosinus en amplitude, en vinkelhastighed og en periodetid.

• Wikimedia Commons har flere filer relateret til Funktion (matematik)