Indskrivelig firkant
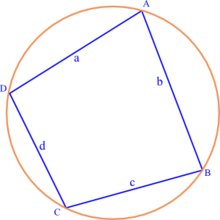
I geometri kaldes en firkant indskrivelig, hvis man kan tegne en cirkel rundt om dem, som indeholder alle fire hjørner. Denne type af firkanter har en række interessante egenskaber, der gør dem anvendelige inden for mange typer af geometriske problemer.
Egenskaber[redigér | rediger kildetekst]
- Om en indskrivelig firkant kan der tegnes en og kun en cirkel, der har alle firkantens hjørner i sin periferi.
- I den indskrivelige firkant ABCD er ∠ABC+∠CDA = ∠BCD+∠DAB = 180◦
- I en indskrivelig firkant ABCD er produktet af diagonalerne lig med summen af produkterne af de to par af modstående sider. Dette er et specialtilfælde af Ptolemæus' ulighed, der for en firkant ABCD siger, at med lighedstegn netop når firkanten er indskrivelig.
- Arealet af en indskrivelig firkant er ud fra Brahmaguptas formel.
At genkende indskrivelige firkanter[redigér | rediger kildetekst]
Når man leder efter indskrivelige firkanter i en geometrisk opgave, er der flere ting man kan kigge efter.
- En firkant ABCD er indskrivelig hvis og kun hvis ∠ACB = ∠ADB.
- En firkant er indskrivelig hvis og kun hvis summen af modstående vinkler er 180◦
- En firkant er indskrivelig hvis begge diagonaler står vinkelret på forlængelsen af hver deres side i firkanten. (Ses ud fra (1))
- Hvis X er skæringspunktet mellem firkant ABCD's diagonaler, da er firkanten indskrivelig hvis og kun hvis AX · XC = BX · XD.
 |
Wikimedia Commons har medier relateret til: |


