Cylindrisk koordinatsystem
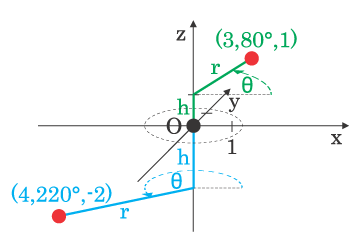
Et cylindrisk koordinatsystem også kaldet et semipolært koordinatsystem, er en type af koordinatsystem indenfor matematikken som udvider idéen for de todimensionale polære koordinater. Denne type af koordinater er primært velegnet til at fremstille cylindere i tre dimensioner.
Tilsvarende for de polære koordinater i det todimensionale tilfælde, udvides denne type af koordinatsystem som sagt ved at tilføje en højde til hver af koordinaterne. Dermed kræver det altså tre parametre for at kunne angive et specifikt punkt. Disse er henholdsvis ρ, som angiver afstanden fra origo til det pågældende punkt. φ som angiver vinklen i forhold til x-aksen i xy-planen. Samt h, som altså angiver den retvinklede afstand fra xy-planen til punktet, op ad z-aksen. Definitionen på punkterne bliver da således:
Eksempel[redigér | rediger kildetekst]
Som allerede nævnt har denne type af koordinater sin styrke i fremstillingen af cylindere, som der her vil blive vist et eksempel på. Man skal således have parametrene til at løbe mellem nogle definerede grænser, så lad os sige at vi ønsker en massiv halvcylinder, med radius 2, og højden 4.

Retvinklede koordinater til semipolære koordinater[redigér | rediger kildetekst]
Ligesom for to dimensioner er det altså muligt at transformere sine kartesiske koordinater til cylindriske koordinater. Dette gøres på følgende måde:
Jacobideterminant[redigér | rediger kildetekst]
Indenfor de semipolære koordinater, kan det lade sig gøre at bestemme Jacobi-determinanten generelt. Dette gøres ved at opstille definitionerne på koordinaterne som vi allerede har gjort, og dernæst opstille det vi kalder Jacobi-matricen. Man kan altså forestille sig at man opstiller definitionerne på koordinaterne i tre søjler i en matrix, for derefter at differentiere første søjle med hensyn til ρ, anden søjle med hensyn til φ og tredje søjle med hensyn til h. Når alt dette er gjort, opstår følgende matrix, som altså som sagt kaldes Jacobi-matricen:
Det er altså denne matrix vi tager determinanten af, når vi finder jacobi-determinanten:
Jacobi-determinanten for semipolære koordinater er altså ganske enkelt ρ.




![{\displaystyle \left.{\begin{matrix}x=\rho \cdot \cos(\varphi )\\y=\rho \cdot \sin(\varphi )\\z=h\end{matrix}}\right\}\quad ,\rho \in [0,2]\quad ,\quad \varphi \in [0,\pi ]\quad ,\quad h\in [0,4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d045e59dda927b091f896cbd76efda1eff0e402)



![{\displaystyle J_{F}(\rho ,\varphi ,h)=\left[{\begin{matrix}\cos \left(\varphi \right)&-\rho \,\sin \left(\varphi \right)&0\\\sin \left(\varphi \right)&\rho \,\cos \left(\varphi \right)&0\\0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ca45acc4d8e55ea0a73b41c03f0b5dcf66d7d0d)
