Buck-konverter

En buck-konverter eller step-down-konverter er en smps med en numerisk output-spænding mindre end dens numeriske input-spænding og input og output har ens fortegn. Boost-konvertere er en klasse af switching-mode power supply (SMPS) indeholdende i sin simpleste form en kommutationscelle; en aktiv kontakt (f.eks. en transistor) og en passiv kontakt (f.eks. en diode) og en spole som energilager. Herudover har buck-konverteren sædvanligvis brug for filtrering udgjort af kondensatorer (mange gange i kombination med spoler) for at mindske output-fluktuationer og især input-fluktuationer (ripple) og EMI.

Figur 1: Buck-konverter diagram.

Den simpleste måde at reducere en DC-spænding er ved at anvende et spændingsdelerkredsløb, men spændingsdelere spilder energi, da de virker ved at "brænde" overflødig energi af som varme; herudover er spændingen ikke reguleret (varierer f.eks. med input-spændingen). I modsætning hertil kan en buck-konverter være temmelig effektiv (let op til 95% for integrerede kredsløb) og selvregulerende, hvilket gør dem anvendelige til opgaver såsom at konvertere en typisk batterispænding på 12-24V i en bærbar computer ned til nogle få volt som mikroprocessoren behøver.

Driftsprincip

Figur 1: Buck-konverter diagram. Nomenklatur.

Det grundlæggende princip, som får buck-konverteren til at virke, er spolens selvinduktion - og herudover den rette timing og miljø.

Når spolen lagrer energi opfører den sig som en belastning og absorberer energi, som lagres i magnetfeltet - og når den afgiver energi, opfører den sig som en energikilde. Spændingen den opretholder under afladningsfasen er præcis så stor, at spolens strøm (relateret til magnetfeltet) opretholdes, og output-spændingen er under normal drift numerisk mindre, men med samme fortegn, men herudover uafhængig af input-spændingen.

Vedvarende/kontinuert strømdrift (CCM)

Figur 2: En buck-konverters to driftstilstande, når drevet i kontinuert strømdrift (CCM). Hvis diskontinuert strømdrift DCM vælges haves en tredje tilstand.

Figur 3: En buck-konverters strøm og spændingsgrafer der drives i kontinuert strømdrift (CCM).

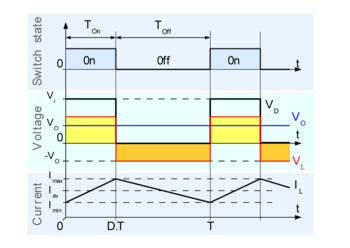
Når en buck-konverter drives i kontinuert strømdrift (CCM), falder strømmen gennem spolen ($I_L$) ikke til nul. Den anvendte nomenklatur er som i figur 1.

Yderligere antagelser i dette afsnit:

• komponenterne har ideel opførsel
• konverteren arbejder i ligevægt
• $V_i$ er konstant
• Output-spændingen $V_o$ er numerisk mindre end input-spændingen $V_i$ (belastningen er passende høj resistans og kondensatoren passende høj kapacitans)
• $V_o$ er konstant, hvilket betyder at kondensatorens kapacitans nødvendigvis er uendelig
• $V_o$ har samme fortegn som $V_i$. Med den viste dioderetning er begge positive.

Figur 3 viser de typiske strøm og spændingsgrafer i en konverter med CCM-drift. En buck-konverters driftstilstande under CCM (se figur 2) er:

• i transistor on-tilstanden (diode off), er S ledende (se figur 1), hvilket resulterer i en stigende spolestrøm over tidsinterval [0;D*T[.
• i transistor off-tilstanden (diode on), er S ikke-ledende og så længe den er det (og der er energi lagret i spolens magnetfelt), vil dioden lede spolens genererede strøm til kondensatoren C og belastningen R. Dette sker over tidsinterval [D*T;T[

Under de tidligere nævnte antagelser kan output-spændingens ligning udledes. Dette gøres i det følgende.

Når S er ledende; on (transistoren er on), vil input-spændingen ($V_i-V_o$) være påtrykt spolen, hvilket resulterer i en linear stigende strøm ($I_L$) løber gennem spolen som funktion af (t), som kan beregnes ved følgende formel:

$\frac{\Delta I_L}{\Delta t}=\frac{V_i-V_o}{L}$

Ved slutningen af S on-perioden, vil stigningen af I_L derfor være:

$\Delta I_{L_{on}}=\int_0^{D T}\frac{V_L}{L}\, dt=\frac{\left(V_i-V_o\right)\cdot D T}{L}$

D er arbejdscyklus (en. duty cycle). D repræsenterer brøkdelen, at S er on i forhold til den totale S on plus S off tid (S on plus S off er her kommutationscyklens tid). Derfor vil D være mellem 0 (S er aldrig on) og 1 (S er altid on).

Når S er off, sender spolen en faldende strøm over tid gennem kondensator og belastning. Under de tidligere antagelser, vil udviklingen af I_L være lineart faldende:

$V_o=L\frac{dI_L}{dt}$

I så fald vil det lineare I_L fald under S off-perioden være:

$\Delta I_{L_{off}}=\int_0^{(1-D) T}\frac{V_L}{L}\, dt=-\frac{V_o\cdot (1-D) T}{L}$

Da vi antager at konverteren drives under ligevægtsbetingelser, bliver energimængden gemt i hver af dets komponenter nødt til at være den samme ved begyndelsen og slutningen af kommutationscyklen. I spolen vil den være givet ved:

$E=\frac{1}{2} L I_L^2$

Derfor vil spolestrømmen, under de givne antagelser, være den samme ved begyndelsen og slutningen af kommutationscyklen. Dette kan skrives som

Therefore, $\Delta I_{L_{on}}+\Delta I_{L_{off}}=0$

Ved at erstatte $\Delta I_{L_{on}}$ og $\Delta I_{L_{off}}$ med deres udtryk giver:

$\frac{\left(V_i-V_o\right)\cdot D T}{L}-\frac{V_o\cdot (1-D) T}{L}=0$

Dette kan skrives som:

$V_o=D\cdot V_i$

Hvilket viser at arbejdscyklus er:

$D=\frac{V_o}{V_i}$

Hvis antagelserne holder, vil output-spændingen stige med D, når arbejdscyklus går fra 0 til 1) - og mod input-spændingen, når D går mod 1. Da D er mindre end eller lig 1, vil output-spændingen numerisk være mindre eller lig input-spændingen. Dette er årsagen til at denne konvertertype også benævnes step-down-konverter.

Diskontinuert strømdrift (DCM)

Figur 4: En buck-konverters strøm og spændingsgrafer der drives under diskontinuert strømdrift (DCM). I en nederste graf er $I_{S}$ rød og $I_{D}$ blå.

Man kan vælge at spolestrømmen skal falde til nul i en del af kommutationscyklen. Den eneste forskel fra CCM-drift er at spolen er tømt for energi i en kort tid (se figur 4). Nomenklatur som i figur 1.

Yderligere antagelser i dette afsnit:

• komponenterne har ideel opførsel
• konverteren arbejder i ligevægt
• $V_i$ er konstant
• Output-spændingen $V_o$ er numerisk mindre end input-spændingen $V_i$ (belastningen er passende høj resistans og kondensatoren passende høj kapacitans)
• $V_o$ er konstant, hvilket betyder at kondensatorens kapacitans nødvendigvis er uendelig
• $V_o$ har samme fortegn som $V_i$. Med den viste dioderetning er begge positive.

En buck-konverters driftstilstande under diskontinuert strømdrift (DCM) (se figur 2) er:

• i transistor on-tilstanden (diode off), er S ledende (se figur 1), hvilket resulterer i en stigende spolestrøm over tidsinterval [0;D*T[.
• i transistor off-tilstanden (diode on), er S ikke-ledende og så længe der er energi lagret i spolens magnetfelt, vil dioden lede spolens genererede strøm til kondensatoren og belastningen R. Dette sker over tidsinterval [D*T;(D+δ)*T[
• i transistor off-tilstanden (diode off), er S ikke-ledende og der er ingen energi lagret i spolens magnetfelt, så dioden er også ikke-ledende. Dette sker over tidsinterval [(D+δ)*T;T[

Det har en effekt på output-spændingens ligning. Den udledes i det følgende.

Da, spolestrømmen ved begyndelsen af kommutationscyklen er nul, vil dens maksimumsværdi $I_{L_{max}}$ (ved $t = D T$) være

$I_{L_{max}}=\frac{V_i-V_o}{L}D\cdot T$

transistor off-tilstanden (diode on), I_L falder til nul efter $\delta T$:

$I_{L_{max}}+\frac{V_o \delta T}{L}=0$

Ved at anvende de to foregående ligninger er δ:

$\delta=\frac{V_i-V_o}{V_o}D$

Belastningsstrømmen I_o er lig diodens middelstrøm (I_D). Som det kan ses på figur 4, er diodestrømmen lig spolestrømmen mens S er off. Derfor kan output-strømmen skrives som:

$I_o=\bar{I_D}=\frac{1}{2}I_{L_{max}}\cdot D +\frac{1}{2}I_{L_{max}}\cdot \delta=\frac{I_{L_{max}}\left(D+\delta\right)}{2}$

Ved at udskifte I_Lmax og δ med deres respektive udtryk fås:

$I_o=\frac{\left(V_i-V_o\right)D\cdot T\left(D+\delta\right)}{2L}$

And substituting δ by the expression given above yields:

$I_o=\frac{\left(V_i-V_o\right)D\cdot T\left(D+\frac{V_i-V_o}{V_o}D\right)}{2L}$

Derfor kan output-spændings-forstærkningsfaktoren skrives som følger:

$\frac{V_o}{V_i}=\frac{1}{\frac{2L\cdot I_o}{D^2\cdot V_i\cdot T}+1}$

Sammenlignet med udtrykket af output-spændingen for CCM-drift, er dette udtryk mere kompliceret. Ydermere vil output-spændings-forstærkningsfaktoren ikke kun afhænge af arbejdscyklus, men også af spolens induktans, input-spændingen, (T) og output-strømmen.

Kilder/referencer

• 3. P. Julián, A. Oliva, P. Mandolesi, and H. Chiacchiarini, “Output discrete feedback control of a DC-DC Buck converter,” in Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE’97), Guimaraes, Portugal, 7-11Julio 1997, pp. 925–930.

• 4. H. Chiacchiarini, P. Mandolesi, A. Oliva, and P. Julián, “Nonlinear analog controller for a buck converter: Theory and experimental results”, Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE’99), Bled, Slovenia, 12 - 16 July 1999, pp. 601–606.

• 5. M. B. D’Amico, A. Oliva, E. E. Paolini y N. Guerin, “Bifurcation control of a buck converter in discontinuous conduction mode”, Proceedings of the 1st IFAC Conference on Analysis and Control of Chaotic Systems (CHAOS’06), pp. 399-404, Reims (Francia), 28 al 30 de junio de 2006.

• 6. Oliva, A.R., H. Chiacchiarini y G. Bortolotto “Developing of a state feedback controller for the synchronous buck converter”, Latin American Applied Research, Volumen 35, Nro 2, Abril 2005, pp. 83-88. ISSN: 0327-0793.

• 7. D’Amico, M. B., Guerin, N., Oliva, A.R., Paolini, E.E. Dinámica de un convertidor buck con controlador PI digital. Revista Iberoamericana de automática e informática industrial (RIAI), Vol 4, No 3, julio 2007, pp. 126-131. ISSN: 1697-7912.

Se også

• Boost-konverter
• Buck-boost-konverter
• Split-pi-konverter (Boost-Buck-konverter)
• DC-til-DC-konvertere

Eksterne henvisninger

• Wikimedia Commons har flere filer relateret til Buck-konverter

• Switch-Mode Power Supply Tutorial - Detailed article on DC-DC converters which gives a more formal and detailed analysis of the Buck including the effects of non-ideal switching (but, note that the diagram of the buck-boost converter fails to account for the inversion of the polarity of the voltage between input and output).
• SPICE simulation of the buck converter.

Many Java applets demonstrating the operation of converters are available on the Interactive Power Electronics Seminar (iPES)