Tangens
Tangens er en trigonometrisk funktion inden for matematikken. Tangens til en vinkel er lig sinus til den pågældende vinkel divideret med cosinus til samme vinkel. Funktionen indførtes af den danske matematiker Thomas Fincke i hans Geometria rotundi (1583).
Funktionen tangens defineres som:[1]
Tangens og den retvinklede trekant[redigér | rediger kildetekst]
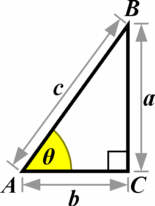
For en retvinklet trekant gælder, at tangens til en af de to vinkler, der ikke er rette, er lig med forholdet mellem vinklens modstående katete og dens hosliggende katete. For trekanten på illustrationen til højre gælder, at tangens til den vinkel θ der er markeret med gul farve, er lig med forholdet mellem længderne af siderne a og b, dvs.:[1]
Afledet funktion[redigér | rediger kildetekst]
Lidt specielt for tangensfunktionen findes der på grund af dens definition faktisk flere forskellige beskrivelser af den afledede funktion. Nedenfor ses de tre forskellige måder man kan beskrive den på. Såfremt man bruger den trigonometriske identitet kan man frembringe en løsning hvor cosinus i anden potens indgår. Denne løsning er desuden en variant af definitionen på en anden trigonometrisk funktion kaldet sekantfunktionen, sec, nemlig kvadratet til den. Man kan også vælge at udføre divisionen hvorved man får en funktion hvorved tangens selv indgår.
Stamfunktion[redigér | rediger kildetekst]
Det ubestemte integral for tangensfunktionen kan også vises at være følgende:
Det indses formodentlig lettest ved at differentiere den definerede stamfunktion. Det gøres her nedenfor, ved hjælp af regnereglen for differentiation af sammensatte funktioner:
Rækkerepræsentation[redigér | rediger kildetekst]
Følgende er Taylorrækken for tangensfunktionen, for udviklingspunkt i 0. B'et der indgår er de såkaldte Bernoullital.
Se også[redigér | rediger kildetekst]
- Tangent (funktionen tangens har navn efter begrebet tangent).
Bog[redigér | rediger kildetekst]
- Holth, Klaus m.fl. (1987): Matematik Grundbog 1. Forlaget Trip, Vejle. ISBN 87-88049-18-3
Referencer[redigér | rediger kildetekst]
| | Spire Denne artikel om matematik er en spire som bør udbygges. Du er velkommen til at hjælpe Wikipedia ved at udvide den. |






