Skabelon:Intorient
Udseende
![]()
This template is used to include the oriented integrals around closed surfaces (or hypersurfaces in higher dimensions), usually in a mathematical formula. They are additional symbols to \oiint and \oiiint which are not yet rendered on wikipedia.
Arguments
[rediger kildetekst]- preintegral the text or formula immediately before the integral
- symbol the integral symbol,
- intsubscpt the subscript below the integral
- integrand the text or formula immediately after the formula
All parameters are optional.
Examples
[rediger kildetekst]- The work done in a thermodynamic cycle on an indicator diagram:
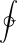
{{intorient
| preintegral=<math>W=</math>
| symbol = varoint
| intsubscpt = <math>{\scriptstyle \Gamma}</math>
| integrand = <math>p{\rm d}V</math>
}}
- In complex analysis for contour integrals:
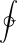
{{intorient|
| preintegral =
|symbol=varoint
| intsubscpt = <math>{\scriptstyle \Gamma}</math>
| integrand = <math>\frac{{\rm d}z}{(z+a)^3z^{1/2}}</math>
}}
- Line integrals of vector fields:


{{intorient|
| preintegral = {{intorient|
| preintegral =
|symbol=oint
| intsubscpt = <math>{\scriptstyle \partial S}</math>
| integrand = <math>\mathbf{F}\cdot{\rm d}\mathbf{r}=-</math>
}}
|symbol=ointctr
| intsubscpt = <math>{\scriptstyle \partial S}</math>
| integrand = <math>\mathbf{F}\cdot{\rm d}\mathbf{r}</math>
}}
- Other examples:

{{Intorient|
| preintegral =
|symbol=oiiintctr
| intsubscpt = <math>{\scriptstyle \Sigma}</math>
| integrand = <math>(E+H\wedge T) {\rm d}^2 \Sigma</math>
}}
{{Intorient|
| preintegral =
|symbol=varoiiintctr
| intsubscpt = <math>{\scriptstyle \Omega}</math>
| integrand = <math>(E+H\wedge T) {\rm d}^4 \Omega</math>
}}
See also
[rediger kildetekst]Non-oriented boundary integrals over a 2-surface and 3-surface can be implemented respectively by:
| Dokumentationen ovenfor er transkluderet fra Skabelon:Intorient/doc. (redigér | historik) Brugere kan eksperimentere i denne skabelons undersider sandkasse (opret | kopiér) og testcases (opret). Tilføj venligst kategorier til /dok-undersiden. Undersider til denne skabelon. |











