Cosinusrelation

Sider og vinkler i en retvinklet trekant

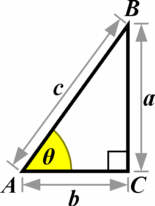
Cosinusrelationer er trigonometriske formler der bestemmer cosinus til vinklerne i en trekant hvori man kender sidernes længder. Kaldes siderne for a, b og c og deres modstående vinkler for hhv. A, B og C skrives formlerne således:

$\cos A={\frac {b^{2}+c^{2}-a^{2}}{2\cdot b\cdot c}}$

$\cos B={\frac {a^{2}+c^{2}-b^{2}}{2\cdot a\cdot c}}$

$\cos C={\frac {a^{2}+b^{2}-c^{2}}{2\cdot a\cdot b}}$

For bestemmelse af sider kan denne omskrivning bruges:

${a^{2}}={b^{2}+c^{2}-2\cdot b\cdot c\cdot \cos A}$

${b^{2}}={a^{2}+c^{2}-2\cdot a\cdot c\cdot \cos B}$

${c^{2}}={a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos C}$

Bemærk at cosinusrelationen gælder for alle trekanter, ikke kun retvinklede trekanter som den på billedet.

For at bruge formlen til noget nyttigt skal man i én af ovenstående ligninger isolere enten en side eller en vinkel på den ene side af lighedstegnet. Løser man ligningen med hensyn til en vinkel, er der i princippet uendeligt mange vinkler hvis cosinus er lig med en given størrelse, men da vinkelsummen i en trekant altid er 180°, er det kun den såkaldt principale løsning (som altid ligger mellem 0 og 180°) der giver mening i trekantberegninger.

Bevis

Bevis for cosinusrelationerne

For at bevise cosinusrelationerne tegner man en trekant, som man deler op i to trekanter (for at få rette vinkler at regne med). Linjen fra vinklen A til siden a = højden (h).

Bevis for cosinusrelationen b² = c² + a² - 2a $\cdot$ c $\cdot$ cos(B) hvis vinkel B er spids:

Med pythagoras får man af den grå trekant: (a - x)² + h² = b² ⇔ h² = b² - (a - x)².

Og tilsvarende af den anden trekant: h² + x² = c² ⇔ h² = c² - x².

Nu er h² isoleret i hver af disse ligninger. De kan derfor sættes lig hinanden:

b² - (a - x)² = c² - x².

Nu skal b² isoleres, derfor får man: b² = c² - x² + (a - x)².

Parenteserne i denne ligning udregnes: b² = c² - x² + a² - 2ax + x².

Dette reduceres til: b² = c² + a² - 2ax.

Vinkel B (i den hvide retvinklede trekant) kan udregnes af: cos(B) = x / c Ved at isolere x i denne ligning får man: x = cos(B) · c.

Da x = cos(B) · c kan man i ligningen b² = c² + a² - 2ax fra før, erstatte x'et med cos(B) · c.

Dvs. b² = c² + a² - 2ax ⇔ b² = c² + a² - 2a · c · cos(B).

Q.E.D

Nu er beviset færdigt.

De andre former af cosinusrelationen bevises på tilsvarende måde.

Se også

• Trekant
• Trekanttilfælde
  • Retvinklet trekant
• Sinusrelationen

Eksterne henvisninger

CosSinCalc - Et online-værktøj, der udregner siderne og vinklerne på en trekant for dig.