Trekant
 For alternative betydninger, se Trekant (flertydig). (Se også artikler, som begynder med Trekant)
For alternative betydninger, se Trekant (flertydig). (Se også artikler, som begynder med Trekant)

En trekant er i geometrisk forstand en polygon med tre vinkler (hjørner) og tre sider. Sider og vinkler omtales under ét som trekantens stykker, og ved hjælp af den matematiske disciplin, der kaldes trigonometri kan man ud fra oplysninger om tre af disse seks stykker (som ikke alle er vinkler) beregne de resterende. Alt afhængig af hvilke oplysninger der er givne, foreligger forskellige trekanttilfælde. Trekantberegning er af stor betydning fordi alle polygoner vha. deres diagonaler kan opdeles i trekanter.
Kategorier af trekanter
[redigér | rediger kildetekst]Trekanter kan inddeles i spidsvinklede, retvinklede og stumpvinklede. I en spidsvinklet trekant er alle tre vinkler mindre end 90°. I en retvinklet trekant er den ene vinkel ret, dvs. lig 90°. I en stumpvinklet trekant er den ene vinkel stump, dvs. større end 90°.
Ligebenet trekant
[redigér | rediger kildetekst]
En ligebenet trekant er en trekant, defineret ved at to af dens tre sider er lige lange. Dermed er to af dens vinkler lige store.
Til højre er vist tre eksempler på ligebenede trekanter: Hver af dem har to indbyrdes lige lange sider (tegnet med blå streg), kaldet trekantens ben. Den sidste side (sort) omtales som grundlinjen.
To af vinklerne i en ligebenet trekant er indbyrdes lige store – det er dem der er markeret med gult på illustrationen, og de omtales som grundvinklerne. Den sidste vinkel (markeret med grønt) kaldes for topvinklen.
Højden på grundlinjen (vist som en stiplet linje i et af eksemplerne) deler topvinklen i to lige store halvdele, og da den også deler grundlinjen i to lige store halvdele, falder den sammen med vinkelhalveringslinjen samt grundlinjens midtnormal og median.
Sætninger om trekanter
[redigér | rediger kildetekst]Der findes et væld af sætninger som udtaler sig om trekanters egenskaber. Kendt af mange er Pythagoras' læresætning. Berømt er også Herons formel, som angiver arealet af en trekant med kendte sider.
En fundamental egenskab ved plane trekanter er at summen af de tre vinkler altid er 180°. Heraf følger f.eks. at en ligesidet trekant er en spidsvinklet trekant (da de tre vinkler er ens, er de alle lig 60°, dvs. spidse).
Arealet af en trekant er givet ved en halv højde gange grundlinje, hvor grundlinjen er (længden af) en af trekantens sider, og højden er (længden af) det linjestykke som står vinkelret på grundlinjen, og som skærer det hjørne som ligger over for grundlinjen.
Areal
[redigér | rediger kildetekst]Arealet af en vilkårlig trekant kan udregnes med formlen:
Hvor A er arealet, h er højden og g er grundlinien. Grundlinien er en trekantens sider. h er et linjestykke vinkelret med g der går fra g til vinklen modstående g.
Alternativt kan man bruge følgende formler:
Hvor T er arealet, a, b og c er givne sider og A, B og C er vinkler. Her gælder det at vinkel A er modstående siden a, vinkel B er modstående siden b og vinkel C er modstående siden c. [2]
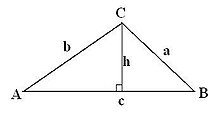
Bevis
[redigér | rediger kildetekst]Vi går ud fra den førstnævnte formel for udregning af arealet i en trekant, hvor grundlinjen er c.
Ved hjælp af sinus får vi
- eller
Dette indsættes i stedet for h.
hvilket også kan skrives som
Der med er anden sætning bevist. Samme fremgangsmåde kan følges for de to andre, hvor man vælger en anden grundlinje.
Areal i en stumpvinklet trekant
[redigér | rediger kildetekst]Ved trekanter, hvor højden falder udenfor trekanten kan formlerne også bruges. Ud fra enhedscirklen vides det, at . Det betyder, at:
Når dette indsættes i udtrykket for arealet, T, fås:
- eller
Altså det samme som før, hvorfor det er bevist, at sætningen gælder for samtlige vilkårlige trekanter.
Indskreven og omskrevne cirkler
[redigér | rediger kildetekst]

Den indskrevne cirkel til en trekant er den største cirkel, der kan indeholdes i trekanten. Cirklen berører alle tre sider. Den omskrevne cirkel til en trekant går gennem trekantens vinkelspidser.
Kilder/referencer
[redigér | rediger kildetekst]Se også
[redigér | rediger kildetekst]| | Søsterprojekter med yderligere information: |
Eksterne henvisninger
[redigér | rediger kildetekst]- CosSinCalc – Et online-værktøj, der udregner siderne og vinklerne på en trekant for dig.











