Boost-konverter
En boost-konverter eller step-up-konverter er en smps med en numerisk output-spænding større end dens numeriske input-spænding og input og output har ens fortegn. Boost-konvertere er en klasse af switching-mode power supply (SMPS) indeholdende i sin simpleste form en kommutationscelle; en aktiv kontakt (f.eks. en transistor) og en passiv kontakt (f.eks. en diode) og en spole som energilager. Herudover har boost-konverteren sædvanligvis brug for filtrering udgjort af kondensatorer (mange gange i kombination med spoler) for at minske input-fluktuationer og især output-fluktuationer (ripple) og EMI.

Supply er en spændingskilde.
Load er en ohmsk belastning.
Overblik[redigér | rediger kildetekst]
Energien kan komme fra DC-kilder såsom batterier, akkumulatorer, solceller, ensrettere og DC-generatorer. En proces som ændrer en DC-spænding til en anden DC-spænding kaldes en DC-til-DC-konverter. En boost-konverter er en DC-til-DC-konverter med en output-spænding større end kilde-spændingen. En boost-konverter kaldes nogle gange en step-up-konverter da den “stepper" kilde-spændingen op. Da elektriske energien og dermed den gennemsnitlige effekt over tid () bevares, er den gennemsnitlige output-strøm mindre end eller lig den gennemsnitlige kilde-strøm.
Driftsprincip[redigér | rediger kildetekst]
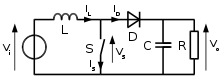
Det grundlæggende princip, som får boost-konverteren til at virke, er spolens selvinduktion – og herudover den rette timing og miljø.
Når spolen lagrer energi opfører den sig som en belastning og absorberer energi, som lagres i magnetfeltet – og når den afgiver energi, opfører den sig som en energikilde. Spændingen den opretholder under afladningsfasen er præcis så stor, at spolens strøm (relateret til magnetfeltet) opretholdes, og output-spændingen er under normal drift numerisk større, men med samme fortegn, men herudover uafhængig af input-spændingen.
Vedvarende/kontinuert strømdrift (CCM)[redigér | rediger kildetekst]


Når en boost-konverter drives i kontinuert strømdrift (CCM), falder strømmen gennem spolen () ikke til nul. Den anvendte nomenklatur er som i figur 1.
Yderligere antagelser i dette afsnit:
- komponenterne har ideel opførsel
- konverteren arbejder i ligevægt
- er konstant
- Output-spændingen er numerisk større end input-spændingen (belastningen er passende høj resistans og kondensatoren passende høj kapacitans)
- er konstant, hvilket betyder at kondensatorens kapacitans nødvendigvis er uendelig
- har samme fortegn som . Med den viste dioderetning er begge positive.
Figur 3 viser de typiske strøm og spændingsgrafer i en konverter med CCM-drift. En boost-konverters driftstilstande under CCM (se figur 2) er:
- i transistor on-tilstanden (diode off), er S ledende (se figur 1), hvilket resulterer i en stigende spolestrøm over tidsinterval [0;D*T[.
- i transistor off-tilstanden (diode on), er S ikke-ledende og så længe den er det (og der er energi lagret i spolens magnetfelt), vil dioden lede spolens genererede strøm til kondensatoren C og belastningen R. Dette sker over tidsinterval [D*T;T[
Under de tidligere nævnte antagelser kan output-spændingens ligning udledes. Dette gøres i det følgende.
Når S er ledende; on (transistoren er on), vil input-spændingen () være påtrykt spolen, hvilket resulterer i en linear stigende strøm () løber gennem spolen som funktion af (t), som kan beregnes ved følgende formel:
Ved slutningen af S on-perioden, vil stigningen af IL derfor være:
D er arbejdscyklus (en. duty cycle). D repræsenterer brøkdelen, at S er on i forhold til den totale S on plus S off tid (S on plus S off er her kommutationscyklens tid). Derfor vil D være mellem 0 (S er aldrig on) og 1 (S er altid on).
Når S er off, sender spolen en faldende strøm over tid gennem kondensator og belastning. Under de tidligere antagelser, vil udviklingen af IL være lineart faldende:
I så fald vil det lineare IL fald under S off-perioden være:
Da vi antager at konverteren drives under ligevægtsbetingelser, bliver energimængden gemt i hver af dets komponenter nødt til at være den samme ved begyndelsen og slutningen af kommutationscyklen. I spolen vil den være givet ved:
Derfor vil spolestrømmen, under de givne antagelser, være den samme ved begyndelsen og slutningen af kommutationscyklen. Dette kan skrives som
Ved at erstatte og med deres udtryk giver:
Dette kan skrives som:
Hvilket viser at arbejdscyklus er:
(gang D med 100 hvis D ønskes i procent)
Hvis antagelserne holder, vil output-spændingen stige med D, når arbejdscyklus går fra 0 til 1) – og teoretisk mod uendelig, når D går mod 1. Dette er årsagen til at denne konvertertype også benævnes step-up-konverter.
Diskontinuert strømdrift (DCM)[redigér | rediger kildetekst]

Man kan vælge at spolestrømmen skal falde til nul i en del af kommutationscyklen. Den eneste forskel fra CCM-drift er at spolen er tømt for energi i en kort tid (se figur 4). Nomenklatur som i figur 1.
Yderligere antagelser i dette afsnit:
- komponenterne har ideel opførsel
- konverteren arbejder i ligevægt
- er konstant
- Output-spændingen er numerisk større end input-spændingen (belastningen er passende høj resistans og kondensatoren passende høj kapacitans)
- er konstant, hvilket betyder at kondensatorens kapacitans nødvendigvis er uendelig
- har samme fortegn som . Med den viste dioderetning er begge positive.
En boost-konverters driftstilstande under diskontinuert strømdrift (DCM) (se figur 2) er:
- i transistor on-tilstanden (diode off), er S ledende (se figur 1), hvilket resulterer i en stigende spolestrøm over tidsinterval [0;D*T[.
- i transistor off-tilstanden (diode on), er S ikke-ledende og så længe der er energi lagret i spolens magnetfelt, vil dioden lede spolens genererede strøm til kondensatoren og belastningen R. Dette sker over tidsinterval [D*T;(D+δ)*T[
- i transistor off-tilstanden (diode off), er S ikke-ledende og der er ingen energi lagret i spolens magnetfelt, så dioden er også ikke-ledende. Dioden er ikke-ledende, fordi output-spændingen er større end input-spændingen (en af antagelserne). Dette sker over tidsinterval [(D+δ)*T;T[
Det har en effekt på output-spændingens ligning. Den udledes i det følgende.
Da, spolestrømmen ved begyndelsen af kommutationscyklen er nul, vil dens maksimumsværdi (ved ) være
transistor off-tilstanden (diode on), IL falder til nul efter :
Ved at anvende de to foregående ligninger er δ:
Belastningsstrømmen Io er lig diodens middelstrøm (ID). Som det kan ses på figur 4, er diodestrømmen lig spolestrømmen mens S er off. Derfor kan output-strømmen skrives som:
Ved at udskifte ILmax og δ med deres respektive udtryk fås:
Derfor kan output-spændings-forstærkningsfaktoren skrives som følger:
Sammenlignet med udtrykket af output-spændingen for CCM-drift, er dette udtryk mere kompliceret. Ydermere vil output-spændings-forstærkningsfaktoren ikke kun afhænge af arbejdscyklus, men også af spolens induktans, input-spændingen, skiftefrekvensen og output-strømmen.
Se også[redigér | rediger kildetekst]
- Buck-konverter
- Buck-boost-konverter
- Split-pi-konverter (patenteret boost-buck-konverter teknologi)
- Cuk-konverter
Yderligere læsning[redigér | rediger kildetekst]
- Mohan, Ned; Undeland, Tore M.; Robbins, William P. (2003). Power Electronics. Hoboken: John Wiley & Sons, Inc. ISBN 0-471-42908-2.
- Basso, Christophe (2008). Switch Mode Power Supplies: SPICE Simulations and Practical Designs. New-York: McGraw-Hill. ISBN 0071508589.


























