Sinusrelation

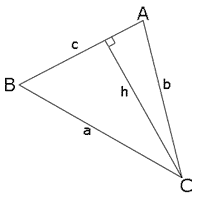
Sinusrelationen er en matematisk formel indenfor trigonometrien, som knytter længden af en trekants sider og størrelsen af dens vinkler sammen i et regneudtryk: Dividerer man længden af en side med sinus til den modstående vinkel, får man samme forholdstal for alle tre "par" af sider og modstående vinkler. Almindeligvis kaldes siderne for a, b og c og deres modstående vinkler for hhv. A, B og C, og med den notation ser formlen således ud:

$\frac{a}{\sin (A)} = \frac{b}{\sin (B)} = \frac{c}{\sin (C)}=2R$

R er radius i trekantens omskrevne cirkel.

For at beregne vinklerne i en trekant kan denne omskrivning bruges:

$\frac{\sin (A)}{a} = \frac{\sin (B)}{b} = \frac{\sin (C)}{c}$

Bemærk at sinusrelationen gælder for alle trekanter.

For at bruge formlen til noget nyttigt, laver man en ligning ud af to af de tre brøker, og isolerer enten en side eller en vinkel på den ene side af lighedstegnet. I sidstnævnte tilfælde fås, at sinus til en vinkel er lig med en given størrelse – og sådan en ligning har to principale løsninger; en stump hhv. en spids vinkel. Af den grund bruger man kun sinusrelationen til at bestemme vinkler i trekanter hvis ikke cosinusrelationerne eller andre formler giver entydige løsninger.

Bevis for sinusrelationerne

• 

  Bevis for sinusrelationerne

Vinklen A i trekanten kan udregnes af: sin(A) = h / b.

Vinklen B i trekanten kan udregnes af: sin(B) = h / a.

Isolerer man h i disse to ligninger får man: sin(A) · b = h og sin(B) · a = h_c.

Disse to ligninger kan man sætte lig hinanden så: sin(A) · b = sin(B) · a.

Dette omskrives til: a / sin(A) = b / sin(B).

For at bevise det sidste led i sinusrelationen (c / sin(C)) gør man det samme, men man sætter bare højden vinkeltret på siden b i stedet for på siden c.

Se også

• Sinus (matematik)
• Trekant
• Trekanttilfælde
  • Retvinklet trekant
• Cosinusrelation

Eksterne henvisninger

CosSinCalc – Et online-værktøj, der udregner siderne og vinklerne på en trekant for dig.