Det gyldne snit

Det gyldne snit handler om at opdele et linjestykke i to stykker, således at forholdet mellem det største og det mindste stykke er lig med forholdet mellem hele linjestykket og det største. På figuren til højre opdeles linjestykket AB i det gyldne snit i punktet s. Det gyldne snit optræder i mange geometriske figurer, bl.a. i et pentagram og en logaritmisk spiral). Desuden dukker det op mange steder i naturen i forbindelse med Fibonaccitallene.
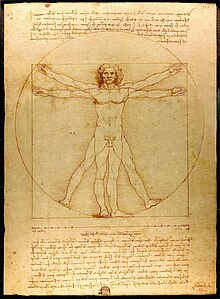
Det gyldne snit kendes også som det guddommelige snit/forhold[kilde mangler] og er anvendt mange steder i kunsthistorien, bl.a. er der forsket i det af Leonardo da Vinci, der forsøgte at påvise, at det gyldne snit ligger til grund for fx menneskets proportioner. Han lavede en version af den vitruvianske mand, Den menneskelige figurs proportioner (som nok er den mest berømte af Leonardo da Vincis tegninger) for at anskueliggøre sin hypotese. Dette bliver dog draget i tvivl.[1]
Matematisk udledning af det gyldne snit[redigér | rediger kildetekst]
Hvis det største liniestykke kaldes a, og det mindste b, kan man ud fra definitionen opstille ligningen:
Ved omskrivning af højresiden fås:
Hvis vi kalder forholdet for , bliver . Ligningen kan derfor udtrykkes i :
Den sidste andengradsligning kalder man det gyldne snits karakteristiske ligning. Med en diskriminant på 5 har den to irrationale tal som løsninger, som vi kalder hhv. og . Tegnet φ er det græske bogstav phi (udtales [fi], ikke at forveksle med π pi). Løsningerne er:
Den første er selvfølgelig den interessante løsning, fordi den er positiv. Den anden er dog også interessant pga. sammenhængen:
Forholdet mellem de to liniestykker i det gyldne snit er altså:
som kan fortolkes på flere måder (husk at 1,6180-1 ≈ 0,6180):
- Det store liniestykke er ca. 61,8% større end det lille stykke.
- Det lille liniestykke udgør ca. 61,8% af det store stykke.
- Hele liniestykket er ca. 61,8% større end det store stykke.
- Det stor liniestykke udgør ca. 61,8% af hele liniestykket.
Endvidere betyder den ovenstående karakteristiske ligning at:
Med tal betyder dette at 1,61802 ≈ 2,6180.

Det gyldne snit kan også foretages symmetrisk, som man ser på figuren til højre, hvor både S og T deler AB i det gyldne snit. Afstanden |ST| vil herved blive a-b. Det viser sig, at T også er det punkt, der deler liniestykket AS i det gyldne snit. Hvis vi antager, at det gælder, ser betingelsen nemlig sådan ud:
som kan omskrives til den oprindelige ligning for det gyldne snit på denne måde:
Potenser af φ og Fibonacci-tallene[redigér | rediger kildetekst]
I dette afsnit udledes nogle af egenskaberne ved φ og især nogle af forbindelserne mellem det gyldne snit og Fibonacci-tallene. Ved anvendelse af den karakteristiske ligning på φ kan vi udvikle flere udtryk for potenser af φ:
Potensen φ3 kan altså skrives som "et helt tal gange φ plus et helt tal". Den samme egenskab kan vi finde ved højere potenser af φ:
Denne udledning kan fortsættes rekursivt i det uendelige, og det viser sig, at koefficienterne i "et helt tal gange φ plus et helt tal" netop er Fibonacci-tallene (0 1 1 2 3 5 8 13 21 osv.), der er defineret ved:
- for
sådan at:
- for
Sammenhængen gælder helt klart for n = 1, for så reduceres sammenhængen til φ = φ. Når n ≥ 2 kan sammenhængen udledes ved induktion, hvis det antages at φn-1 = Fn-1φ + Fn-2:
Fibonacci-tallene udtrykt ved φ[redigér | rediger kildetekst]
Da den karakteristiske ligning gælder for både φ og φ' , gælder begge sammenhængene:
- og
- for
Trækkes de to ligninger fra hinanden, får vi:
Her kan vi isolere det n'te Fibonacci-tal:
Fibonacci-tallene kan altså udtrykkes ved hjælp af forholdene ved det gyldne snit. Med andre ord kan de udregnes ved formlen:
Pentagrammet og beslægtede figurer[redigér | rediger kildetekst]
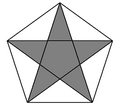
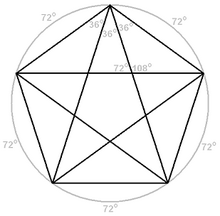
Et af stederne, hvor det gyldne snit optræder, er i en regulær femtakket stjerne, et pentagram. En sådan ses på på figuren til venstre omskrevet af en regulær femkant, en pentagon. Til højre er desuden indtegnet den omskrevne cirkel, og alle relevante vinkler er indtegnet. De fem vinkelbuer vil alle være på 360°/5 = 72°. Derfor er den spidse vinkel på en tak og dens to nabovinkler alle 72°/2 = 36°. Den spidsvinklede trekant i takken er ligebenet, så de to andre vinkler i trekanten vil være (180°-36°)/2 = 72°. De stumpe vinkler ved siden af disse vinkler vil være 180°-72° = 108°.

Det gyldne snit i pentagrammet[redigér | rediger kildetekst]
På figuren til højre har vi nu indført sidelængden a som længden på en tak og b som sidelængden på femkanten i midten af pentagrammet. Det viser sig at forholdet a/b netop er det gyldne snit.
Udregninger af vinklerne medfører, at de to trekanter i figuren til venstre, ΔQPR og ΔQTS, er ensvinklede. Hvis vi derfor tager forholdene mellem ensliggende sider i hhv. den store (svagt lyserøde) og den lille (stærkt lyserøde) trekant, kommer vi frem til følgende:
Med sidelængderne indført, bliver det:
Dette er nøjagtig samme ligning, som vi brugte til at definere det gyldne snit med, og derfor deles f.eks. liniestykket PS i det gyldne snit af punktet R.

Gyldne trekanter[redigér | rediger kildetekst]
De to spidsvinklede trekanter, ΔQPR og ΔQTS, men også den stumpvinklede trekant, ΔRSQ, siges alle at være gyldne trekanter, fordi forholdet mellem deres sider er tallet φ. For de spidsvinklede trekanter fremkommer det som forholdet mellem et ben og grundlinien; for den stumpvinklede trekant er det forholdet mellem grundlinien og et ben.
Også de store stumpvinklede trekanter med top i et hjørne af femkanten og de to hosliggende sider i femkanten som ben og en diagonal i femkanten som grundlinie er gyldne. Derfor er forholdet mellem en diagonal og en side i en regulær femkant tallet φ.
Gyldne trekanter ses også i en regulær tikant som den der ses i figuren til højre, hvor den er tegnet ind oven på et pentagram. Her er buelængden mellem hvert hjørne i tikanten nu 36°, og derfor er de ti trekanter med toppunkt i figurens centrum ensvinklede med ΔQPR i pentagrammet ovenfor og altså gyldne trekanter. Hvis vi kalder radius i tikantens omskrevne cirkel for r og tikantens sidelængde for s, kan man altså udtrykke følgende sammenhæng mellem r og s:
- .
Andre sammenhænge[redigér | rediger kildetekst]
![]() Dette afsnit eller denne liste er kun påbegyndt. Hvis du ved mere om emnet, kan du hjælpe Wikipedia ved at tilføje mere.
Dette afsnit eller denne liste er kun påbegyndt. Hvis du ved mere om emnet, kan du hjælpe Wikipedia ved at tilføje mere.
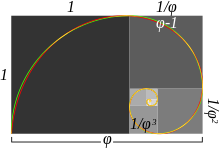
Phi har relation til fibonaccitalfølgen (1 1 2 3 5 8 13 21 osv.), fordi kvotienten af to naboelementer gradvist nærmer sig (konvergerer mod) tallet phi. Jo højere værdi, to naboelementer har, des mere nøjagtigt vil deres kvotient beskrive phi, og hvis naboelementernes værdi er 987 eller højere, vil unøjagtigheden være mindre end ±0,00001.
Phi anses af nogle – f.eks. H.E. Huntley : The Divine Proportion – for at være det smukkeste talforhold i verden. Modpolerne udgøres bl.a. af den amerikanske matematiker George Markowsky, som ikke mener at det gyldne snit kan anerkendes som specielt harmonisk, og af den tyske fysiker Peter Richter, som ved sin forskning i ulineære tilstande i naturen (fraktaler) igen og igen er stødt på netop phi.
Se også[redigér | rediger kildetekst]
Eksterne henvisninger[redigér | rediger kildetekst]
- Alt om Phi Arkiveret 5. december 2006 hos Wayback Machine
- The Golden Museum (engelsk og russisk) Arkiveret 5. april 2019 hos Wayback Machine
- Peter H. Richters hjemmeside Arkiveret 30. december 2004 hos Wayback Machine
- Det Gyldne Snit Arkiveret 1. marts 2016 hos Wayback Machine
- pentagrammet og phi Arkiveret 18. december 2004 hos Wayback Machine
Kilder[redigér | rediger kildetekst]



































