Kosmisk afstandsstige
Denne artikel behøver tilretning af sproget. Sproget i denne artikel er af lav kvalitet på grund af stavefejl, grammatikfejl, uklare formuleringer eller sin uencyklopædiske stil. (maj 2016) (Lær hvordan og hvornår man kan fjerne denne skabelonbesked) |

- Lysegrønne kasser: Metoder der kan anvendes på stjernedannende galakser.
- Lyseblå kasser:Metoder der kan anvendes på Population II galakser.
- Lyselilla kasser: Geometric distance technique.
- Lyserøde kasser: The planetary nebula luminosity function technique is applicable to all populations of the Virgo Supercluster.
- Linjer: Well calibrated ladder step.
- Stiplede linjer: Uncertain calibration ladder step.
Den kosmiske afstandsstige (også kendt som den “ekstragalaktiske afstandsskala”) er den rækkefølge af metoder, som bruges af astronomer til at bestemme afstanden til himmellegemer. En “direkte” afstandsmåling for et astronomisk objekt er kun muligt for de objekter, der er "tæt nok på" (inden for en afstand af nogle tusind parsec) fra Jorden. Metoderne til at bestemme afstande til fjernere objekter er alle baserede på forskellige målte sammenhænge mellem metoder, der virker for korte afstande og metoder, der virker for større afstande. Adskillige metoder afhænger af ”standardlyskilder”, hvilket er et astronomisk objekt med en kendt luminositet.
Stigeanalogien fremkommer fordi ingen enkelt metode kan måle afstande på alle de skalaer, som forekommer i astronomi. I stedet kan en metode bruges til at måle nære afstande, en anden kan bruges til nære og mellemstore afstande osv. Hvert trin på stigen giver information, som kan bruges til at bestemme afstande på det næsthøjeste trin.
Direkte måling[redigér | rediger kildetekst]

Nederst på stigen er fundamentale afstandsmålinger, hvor afstande måles direkte, uden at lave fysiske antagelser omkring det aktuelle objekt. Den præcise måling af en stjernes beliggenhed er en del af disciplinen astrometri.
Astronomisk enhed[redigér | rediger kildetekst]
Direkte afstandsmåling er baseret på den Astronomiske enhed (AE), som er afstanden mellem Jorden og Solen. Historisk, var observationer af Venuspassager vigtige i bestemmelsen af AE; I den første halvdel af det 20. århundrede, var observationer af asteroider også vigtige.
For nuværende er Jordens bane bestemt med stor præcision ved hjælp af radarmåling af afstanden til Venus og andre nære planeter og asteroider,[1] og ved at følge interplanetare rumfartøjer i deres kredsløb rundt om Solen gennem Solsystemet. Keplers Love giver præcise forhold for størrelserne af banerne for objekter, der kredser om Solen, men giver ingen måling af den overordnede skala. Radar bruges til at måle afstanden mellem Jordens bane og banen for et andet objekt. Fra denne måling og forholdet mellem de to banestørrelser, findes størrelsen af Jordens bane. Jordens bane er kendt med en præcision på få meter.
Parallakse[redigér | rediger kildetekst]
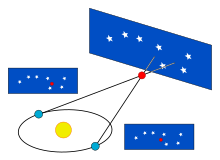
Den vigtigste fundamentale afstandsmåling kommer fra den trigonometriske parallakse. Når Jorden kredser om Solen, så vil positionen af nære stjerner synes at skifte lidt set imod baggrunden. Disse skift er vinkler i en ligebenet trekant, med 2 AE (afstanden mellem de to yderpunkter i Jordens bane om Solen), som grundlinje og afstanden til stjernen som benlængder. Størrelsen af dette skift er ret lille, 1 buesekund for objekter med en afstand på 1 parsec (3.26 light-years) , svarende til de nærmeste stjerner, og mindre som afstanden øges. Astronomer udtrykker normalt afstande i parsec (parallakse buesekunder); lysår bruges i populære fremstillinger.
Da parallakser bliver mindre for større afstande, kan man kun lave brugbare målinger for stjerner med en parallakse, der er nogle få gange større end målenøjagtigheden. Parallaksemålinger har typisk en målenøjagtighed I størrelsesordenen milli-buesekunder. [2] I 1990'erne indsamlede Hipparcos missionen parallakser for over et hundrede tusind stjerner med en præcision på omkring et milli-buesekund,[3] hvilket gav brugbare afstandsbestemmelser for stjerner op til nogle få hundrede parsec. Hubble teleskopet WFC3 har nu potentialet til at måle med en præcision på 20 til 40 micro-buesekunder, hvilket giver pålidelige afstandsmålinger op til 5.000 parsecs (20.000 ly) for et mindre antal stjerner.[4] I begyndelsen af 2020'erne kan GAIA rum-missionen give tilsvarende præcise afstande til alle moderat klare stjerner.
Stjerner har en fart relativt til Solen, som giver egenbevægelse (tværs over himlen) og radialfart (bevægelse mod eller væk fra Solen). Den førstnævnte måles ved at plotte stjernens skiftende positioner over mange år, mens den sidstnævnte findes ved måling af Dobbler-skiftet af stjernens spektrum, som skyldes bevægelsen langs synslinjen.
For en gruppe af stjerner med den samme spektralklasse og en sammenlignelig størrelsesorden, kan man udlede en middelparallakse ved statistisk analyse af forholdet mellem egenbevægelsen og radialfarten. Denne metode er brugbar til at måle afstande for klare stjerner over 50 parsec og store variable stjerner, inklusive Cepheider og RR Lyrae variable stjerner.[5] Bevægelsen af Solen gennem rummet giver en større grundlinje, som øger nøjagtigheden af parallaksemålinger, dette er kendt som sekulær parallakse. For stjerner i Mælkevejen, svarer det til en grundlinje på 4 AE per år, mens den for halo stjerner er 40 AE per år. Efter nogle årtier, kan grundlinjen være flere størrelsesordener større end Jord-Sol grundlinjen, som bruges til traditionel parallaksemåling. Men sekulær parallakse introducerer en højere grad af usikkerhed, fordi den relative fart af andre stjerner er en ubekendt størrelse. Når denne metode bruges på samlinger af flere stjerner, kan man mindske usikkerheden. Usikkerheden er omvendt proportional med kvadratroden af stikprøven. [6]
Moving cluster parallakse er en teknik, hvor bevægelsen af individuelle stjerner I en nærliggende stjernehob kan bruges til at finde afstanden til hoben. Kun åbne stjernehobe er tæt nok på til at denne teknik er anvendelig.
Specielt har bestemmelsen af afstanden til Hyaderne været et vigtigt trin i den kosmiske afstandsstige. For andre individuelle objekter, kan man lave fundamentale afstandsestimater under specielle omstændigheder. Hvis udvidelsen af en gassky, som f.eks. en supernovarest eller en planetarisk tåge, kan observeres over tid, så kan en ”udvidelsesparallakse” afstand til skyen estimeres. En afvigelse af objektet fra kugleform vil give usikkerheder i bestemmelsen. Binære stjerner som er både visuelt og spektroskopisk binære kan man også finde afstanden til med lignende metoder, og der er der ikke den førnævnte geometriske usikkerhed.
Fællestrækket for disse metoder er, at en måling af vinkelbevægelse kombineres med en måling af den absolutte hastighed, normalt via Doppler effekt.
Afstandsestimaterne kommer fra at beregne hvor langt objektet må være væk, for at den observerede absolutte hastighed giver den observerede vinkelbevægelse. Udvidelses parallakser kan især give grundlæggende afstandsestimater for objekter som er meget langt væk, fordi materiale udskudt fra supernovaer har store udvidelses hastigheder og store størrelser (sammenlignet med stjerner). Desuden kan de observeres med radio interferometri, som kan måle meget små vinkelbevægelser. Disse målinger kombineres til at give grundlæggende afstandsestimater til supernovaer I andre galakser. [7] Selv om de er værdifulde, så er sådanne tilfælde ret sjældne, så de bruges primært til at kontrollere de afstandsestimater der er lavet med andre metoder.
Standardlyskilder[redigér | rediger kildetekst]
Næsten alle astronomiske objekter, der bruges som fysiske afstands indikatorer tilhører en eller anden klasse med en kendt lysstyrke. Ved at sammenligne denne kendte lysstyrke med den observerede lysstyrke, kan afstanden findes med afstandskvadratloven. Disse objekter med kendt lysstyrke kaldes ”standardlyskilder”. Klarheden af en stjerne kan udtrykkes ved dens absolutte størrelsesklasse. Denne størrelse findes fra logaritmen af stjernen som den ville ses, hvis den lå i 10 parsec afstand fra Jorden. Den tilsyneladende størrelsesklasse, eller størrelsesklassen set af en observatør (man bruger et såkaldt bolometer), kan måles og bruges sammen med den absolutte størrelsesklasse til at finde afstanden D til objektet i kiloparsec (hvor 1 kpc er lig 1000 parsecs) som følger:
or
Hvor m er den tilsyneladende størrelsesklasse og M den absolutte. For at dette skal være præcist, skal begge størrelsesklasser måles for den samme frekvens og der må ikke være nogen relativ bevægelse i radialretningen. Der skal også bruges en metode til at tage højde for interstellar dæmpning, som også får objekterne til at synes svagere og mere rødlige, specielt hvis objektet ligger I et støvet eller gasfyldt område.[8] Forskellen mellem den absolutte og den tilsyneladende størrelsesklasse kaldes afstandsmodulet, og astronomiske afstande, specielt mellem galakser opgives nogle gange på den måde.
Vanskeligheder[redigér | rediger kildetekst]
Der findes to vanskeligheder for enhver type af standardlyskilder. Den væsentligste er kalibreringen, det er bestemmelsen af den præcise absolutte størrelsesklasse for lyskilden. Dette omfatter at klassen skal være defineret så præcist, at medlemmer af den kan identificeres, og at finde nok medlemmer af klassen med en kendt afstand, således at deres sande absolutte størrelsesklasse kan findes med tilstrækkelig nøjagtighed.
Den anden er at genkende et medlem af klassen, og ikke ved en fejl bruge den på et objekt, der ikke tilhører klassen.
På ekstreme afstande, hvor man mest har brug for en afstandsindikator, kan dette genkendelsesproblem være ret alvorligt. Et væsentligt forbehold ved standardlyskilder er det tilbagevendende spørgsmål om hvor standardiserede de faktisk er.
F.eks. synes alle observationer at vise, at Type Ia supernovaer, der har en kendt afstand, har samme lysstyrke (korrigeret for lyskurvens facon). Baggrunden for denne ensartethed i lysstyrke er beskrevet herunder; men der foreligger den mulighed at fjerne Type Ia supernovaer har andre egenskaber end de nære Type Ia supernovaer Brugen af Type Ia supernovaer er afgørende I bestemmelsen af den rigtige kosmologisk model. Hvis der rent faktisk er en forskel i egenskaberne for Type Ia supernovaer over lange afstande, så kan dette medføre fejlskøn af de kosmologiske parametre, specielt i vurderingen af stoftæthedsparameteren .[9][bør uddybes]
At dette ikke kun er et filosofisk spørgsmål, kan ses fra den historiske afstandsmåling med brug af Cepheide variable. I 1950’erne, opdagede Walter Baade at de nærliggende Cepheide variable, der blev brugt til at kalibrere standardlyskilderne var af en anden type end dem, der blev brugt til at måle afstande til nærtliggende galakser. De nære Cepheide variable var population I stjerner med meget højere metalindhold end de fjerne population II stjerner. Derfor var population II stjernerne faktisk meget mere lysstærke end formodet, og det havde den effekt af fordoble alle afstande til stjernehobe, de nære galakser og Mælkevejens diameter.
Galaktiske afstandsindikatorer[redigér | rediger kildetekst]
Med få undtagelser er afstande baseret på direkte måling kun til rådighed ud til omkring 1000 parsec, hvilket er en beskeden del af vores egen galakse. For fjernere afstande, baserer målingerne sig på fysiske antagelser, som er, at man genkender det aktuelle objekt, og at klassen af objekter er ensartet nok til at dets medlemmer kan bruges til en meningsfuld estimering af afstanden. Fysiske afstandsindikatorer, som bruges på stadigt større skala, omfatter :
- Dynamisk parallakse, anvendelse af baneparametre for visuelle binære til at måle massen af systemet og masse-luminositets relationen til at bestemme luminositet.
- Gensidigt formørkende binære — I det sidste årti, er målinger af gensidigt formørkende binæres fundamentale parametre blevet mulige med 8—meter teleskoper. Dette gør dem egnede som afstandsindikatorer. For nylig, er de blevet brugt til at give et direkte afstandsestimat til den store Magellanske sky, Den lille Magellanske sky, Andromedagalaksen og Trekantgalaksen. Gensidigt formørkende binære giver en direkte metode til at måle afstande til galakser med 5% nøjagtighed op til omkring 3 Mpc (3 million parsec), med dagens teknologi. [10]
- RR Lyra variable— bruges inden for Mælkevejen og til nærliggende stjernehobe.
- De følgende fire indikatorer bruger alle stjerner i den gamle population (Population II):[11]
- spidsen af kæmpegrenen (SAKG) afstands indikator
- Planetarisk tåge luminositets funktion (PTLF)
- Kugleformet stjernehob luminositets funktion (KSLF)
- Overflade lysstyrke fluktuation (OLF)
- I galaktisk astronomi bruges X-ray bursts (termonukleare udbrud fra overfladen af en neutronstjerne) som standard lyskilde. Observationer af røntgen udbrud viser til tider røntgenspektre, der er forskudt af ekspansion. Røntgenfluxen vil i dette tilfælde ved toppen af udbruddet svare til Eddington luminositeten, der kan beregnes når massen af neutronstjernen er kendt (1.5 solmasser er en almindelig antagelse). Denne metode giver mulighed for at finde afstanden til nogle røntgenudsendende dobbeltstjerner med lav masse. Disse stjerner lyser svagt i synlige bøgelængder, hvilket gør det svært at finde afstanden med målinger i synligt lys og derfor er røntgenmålingerne så nyttige.
- Interstellare masere kan bruges til at finde afstanden til galaktiske og nogle ekstragalaktiske objekter, der har maseremission.
- Cepheider og supernovaer
- Individuelle galakser i galaksehobe
- Tully–Fishers relationen
- Faber–Jacksons relationen
- Type Ia supernovaer, som har en meget veldefineret maksimal absolut størrelsesklasse som en funktion af faconen af deres lyskurve, er meget nyttige til at finde ekstragalaktiske afstande op til nogle få hundrede Mpc.[12] En bemærkelsesværdig undtagelse er SN 2003fg, "Champagne Supernovaen", en Type Ia supernova af en usædvanlig slags.
- Rødforskydning og Hubbles lov
Hovedserie tilpasning[redigér | rediger kildetekst]
Når den absolutte størrelsesklasse for en gruppe stjerner afbildes mod spektralklassen for stjernen I et Hertzsprung-Russell-diagram, kan man se udviklingsmønstre der har sammenhæng med masse, alder og sammensætning af stjernen. Specielt gælder der, at gennem den hydrogenforbrændende periode, ligger stjerner langs en kurve i diagrammet som kaldes hovedserien. Ved at måle disse egenskaber fra stjernens spektrum, kan placeringen af en stjerne I H-R diagrammet bestemmes, og dermed kan man anslå stjernens absolutte størrelsesklasse.En sammenligning med værdien af dens tilsyneladende størrelsesklasse muliggør bestemmelse af den omtrentlige afstand, efter at der er korrigeret for interstellar dæmpning af lyset fra støv og gas. I en gravitationeltbundet stjernehob som Hyaderne, blev stjernerne dannet nogenlunde samtidigt og ligger i den samme afstand. Dette muliggør en ret nøjagtig hovedserietilpasning, der giver både alder og afstandsbestemmelse.
Ekstragalaktisk afstandsskala[redigér | rediger kildetekst]
| Metode | Usikkerhed for enkelte galakser (Mpc) | Afstand til Virgohoben (Mpc) | Rækkevidde (Mpc) |
|---|---|---|---|
| Klassiske cepheider | 0.16 | 15–25 | 29 |
| Novaer | 0.4 | 21.1 ± 3.9 | 20 |
| Planetarisk tåge luminositets funktion | 0.3 | 15.4 ± 1.1 | 50 |
| Kuglehobs luminositets funktion | 0.4 | 18.8 ± 3.8 | 50 |
| Overflade lys-styrke fluktuation | 0.3 | 15.9 ± 0.9 | 50 |
| D–σ relation | 0.5 | 16.8 ± 2.4 | > 100 |
| Type Ia Supernovaer | 0.10 | 19.4 ± 5.0 | > 1000 |
Den ekstragalaktiske afstandsskala er en række af metoder, som bruges I dag af astronomer til at finde afstande af kosmologiske legemer uden for vores egen galakse, som ikke nemt kan findes med traditionelle metoder. Nogle metoder udnytter egenskaber ved objekter, såsom stjerner, kuglehobe, tåger, og hele galakser. Andre metoder baseres mere på statistik og sandsynlighed for f.eks. hele galaksehobe.
Wilson–Bappu-effekten[redigér | rediger kildetekst]
“Wilson-Bappu-effekten”, som blev opdaget i 1956 af Olin Wilson og M.K. Vainu Bappu, udnytter effekten kendt som spektroskopisk parallakse. Visse stjerner har træk i deres emission/absorptions spektre, der tillader relativt enkel udregning af den absolutte størrelsesklasse. Visse spektrallinjer er direkte forbundet med et objekts størrelsesklasse, som f.eks. K absorptions linjen i kalcium. Afstanden kan så beregnes fra afstandsmodulus:
Selv om denne metode I teorien har evnen til at give pålidelige afstandsbedømmelser for stjerner ud til ca. 7 megaparsec (Mpc), bruges den normalt kun for stjerner i kiloparsec (kpc) afstand.
Metoden er kun sikker for stjerner over størrelsesklasse 15.
Klassiske Cepheider[redigér | rediger kildetekst]
Når man kommer uden for rækkevidden af Wilson–Bappu effekten, så er den næste metode, som bygger på periodeluminositets sammenhængen for klassiske Cepheide variable . Den følgende sammenhæng kan bruges til at beregne afstande for galaktiske og ekstragalaktiske klassiske Cepheider:
Adskillige problemer komplicerer brugen af Cepheider som standardlyskilder og bliver aktivt debatteret, især de følgende: arten og lineariteten for periodeluminositets relationen i forskellige bånd og virkningen af metalliciteten på både nulpunket og hældningen af disse relationer, og virkningerne af lysforurening og en skiftende og typisk ukendt dæmpningslov for måling af Cepheide afstandene. [16][17][18][19][20][21][22][23][24]
Disse uafklarede spørgsmål har resulteret i citerede værdier for Hubble konstanten mellem 60 km/s/Mpc og 80 km/s/Mpc. Afklaringen af disse uoverensstemmelser er en af de vigtigste problemer i astronomi da de kosmologiske parametre for universet kan være bundet til den præcise værdi af Hubbles konstant.[25] [26]
Cepheide variable stjerner var det vigtigste redskab i Edwin Hubble’s konklusion fra 1923 at M31 (Andromeda) var en ekstern galakse og ikke en mindre tåge i Mælkevejen. Han beregnede afstanden M31 til 285 Kpc, den nuværende værdi er 770 Kpc.
Den fjernest kendte Cepheide er i NGC 3370, en spiral galakse i stjernebilledet Løven, afstanden er 29 Mpc.
Cepheide variablee stjerner er på ingen måde perfekte afstands markører.
Supernovaer[redigér | rediger kildetekst]

Der er flere forskellige metoder med hvilke supernovaer kan bruges til at måle ekstragalaktiske afstande.
Måling af en supernovas fotosfære[redigér | rediger kildetekst]
Vi kan antage at en supernova udvider sig kugleformet symmetrisk. Hvis supernovaen er tæt nok på, så man kan måle vinkeludstrækningen , θ(t), af dens fotosfære, kan man bruge ligningen
hvor ω er vinkelhastigheden, θ er vinkeludstrækningen. For at få nøjagtige målinger er det nødvendigt at lave to observationer adskilt i tiden Δt. Efterfølgende bruges at
hvor d er afstanden til supernovaen, Vej er radialhastigheden af den udslyngede masse (det kan antages at Vej er lig Vθ , hvis der er kuglesymmetri).
Denne metode virker kun hvis supernovaen er tæt nok på til at man kan måle nøjagtigt på dens fotosfære. Tilsvarende må man tage i betragtning af skallen af ekspanderende gas ikke er helt kugleformet og heller ikke et perfekt sortlegeme.
Interstellar dæmpning kan yderligere forhindre nøjagtige målinger. Desuden er der yderligere vanskeligheder med at måle på supernovaer, der følger en kernekollaps. Alle disse faktorer bidrager til en fejl på op til 25 % i afstandsbestemmelsen.
Type Ia lyskurver[redigér | rediger kildetekst]
Type Ia supernovaer er en af de bedste metoder til at finde ekstragalaktiske afstande. Ia'er opstår når en hvid dværg i et dobbeltstjernesystem begynder at samle materiale fra sin ledsagestjerne. Når den hvide dværg samler stof, så vil den til sidst nå sin Chandrasekhar grænse på .
Når denne grænse først er nået, bliver stjernen ustabil og gennemgår en lavineagtig kernefusion reaktion.
Fordi alle Type Ia supernovaer eksploderer ved næsten den samme masse, har de samme absolutte størrelsesklasse.
Dette gør dem meget værdifulde som standardlyskilder. Alle Type Ia supernovaer har en standard blå og visuel størrelsesklasse
Hvis det derfor er muligt at bestemme dens maksimale størrelsesklasse, når man observerer en Type Ia supernova, så kan man beregne dens afstand.
Det er ikke ubetinget nødvendigt at fange supernovaen direkte ved dens spids størrelsesklasse; man kan bruge multicolor light curve shape metoden (MLCS), formen af lyskurven (taget en rimelig tid efter eksplosionen) sammenlignes med en familie af parametriserede kurver, der så vil angive den absolutte størrelsesklasse ved den maksimale lysstyrke. Denne metode tager også højde for interstellar dæmpning.
På tilsvarende vis tilpasses med stretch metoden den specielle lyskurve til en skabelon lyskurve. Denne skabelon, er i modsætning til ved MLCS kun en enkelt lyskurve, som er blevet strakt eller komprimeret i tid. Ved at bruge Stretch faktoren kan spids størrelsesklassen bestemmes.[kilde mangler]
Anvendelsen af Type Ia supernovaer er en af de mest nøjagtige metoder, især fordi supernova eksplosioner kan ses over over store afstande (deres luminositeter er på højde med de galakser som de er i), meget længere væk end Cepheiderne (500 gange længere væk). Meget tid er blevet anvendt til at forfinde denne metode. Den nuværende usikkerhed nærmer sig bare 5 %, svarende til en usikkerhed på kun 0,1 størrelsesklasser.
Novaer i afstandsbestemmelser[redigér | rediger kildetekst]
Novaer kan bruges på næsten den samme måde som supernovaer til at bestemme ekstragalaktiske distancer. Der er en direkte sammenhæng mellem en novas maksimale størrelsesklasse og den tid det tager for dens synlige løs af aftage to størrelsesklasser:
Hvor er den tidsafledede af novaens størrelsesklasse, den beskriver det gennemsnitlige fald over de 2 første størrelsesklasser.
Efter at novaer dør ud, er de omtrent så lysstærke som de mest lysende Cepheider, derfor har begge disse metoder den sammen max afstand de virker på: ~ 20 Mpc. Fejlen med denne metode er omkring ±0.4 i størrelsesklasse.
Kuglehobes luminositetsfunktion[redigér | rediger kildetekst]
Metoden med at anvende kuglehobes luminositetsfunktionen, der er baseret på at sammenligne luminositeter af kuglehobe (som ligger i galaktiske haloer ) fra fjerne galakser med Virgo hoben, giver en usikkerhed på ca. 20 % i bestemmelsen af distancerne (svarende til ca. 0.4 størrelsesklasser).
US astronomen William Alvin Baum prøvede først at bruge en lignende metode til at måle fjerne elliptiske galakser. Han sammenlignede de klareste kuglehobe i Virgo A galaksen med dem i Andromeda, idet han antog at luminositeten af hobene var den samme i begge. Da han kendte afstanden til Andromeda, kunne han finde Virgo A’s afstand.
Baum brugte en enkelt kuglehob, men enkelthobe er ofte dårlige standardlyskilder.
Den canadiske astronom René Racine antog at brugen af kuglehobs luminositets funktionen (KLF) ville give en bedre tilnærmelse.
Antallet af kuglehobe som en funktion af størrelsesklasse er:
hvor m0 er turnover størrelsesklassen, M0 er størrelsesklassen af Virgo hoben og sigma er dispersionen ~ 1.4 mag.
Det er vigtigt at huske, at det antages, at kuglehobe alle har den samme luminositet i universet.
Dette til trods for, at der ikke findes en universel sammenhæng, som gælder for galakser.
Planetarisk tåge luminositetsfunktion[redigér | rediger kildetekst]
På samme måde som KLF-metoden, kan en tilsvarende numerisk analyse bruges for planetariske tåger i fjerne galakser.
Metoden med lat bruge en planetarisk tåge luminositetsfunktion (PTLF) blev fremsat i de sene 70'ere af Holland Cole og David Jenner. De antog at alle planetariske tåger har ens maksimale absolutte størrelsesklasser, der nu er beregnet til at være M = −4.53.
De kunne derfor bruges som standardlyskilder.
Astronomen George Howard Jacoby og hans kollega foreslog senere at PTLF funktionen var:
Hvor N(M) er antallet af planetariske tåger med absolut størrelsesklasse M. M* er tågen med den klareste størrelsesklasse.
Overfladelysstyrke fluktuations metoden[redigér | rediger kildetekst]

Denne metode kan med varierende fejlprocenter bruges til at lave afstandsbedømmelser ud over 100 Mpc, selv om den ofte anvendes mere lokalt.
Overfladelysstyrke fluktuations (OLF) metoden udnytter brugen af CCD kameraer i teleskoper. På grund af rumlige fluktuationer i en galakses overfladeklarhed, vil nogle pixels i disse kameraer opsamle flere stjerner end andre. Men, som afstanden vokser, vil billedet blive mere og mere jævnt. Analyse af dette beskriver størrelsesordenen af pixel-til-pixel variationen, som er et direkte mål for afstanden til galaksen.
Overlap og skalering[redigér | rediger kildetekst]
En kæde af afstands indikatorer, som udgør afstandsstigen, er nødvendigt for at finde afstanden til andre galakser.
Årsagen er, at objekter som er klare nok til at kunne genkendes og måles på sådanne afstande er sjældne. Der er derfor også kun ganske få der er nære nok til at man kan finde den nøjagtige afstand med parallaksemetoden. Derfor kan man ikke kalibrere denne type af afstandsindikatorer direkte.
F.eks. kan Cepheider, der er nogle af den bedste indikatorer for nærtliggende spiralgalakser, endnu ikke kalibreres med parallaksemetoden alene.
Situationen kompliceres af den kendsgerning, at forskellige stjernepopulationer i almindelighed ikke har alle typer af stjerner i sig.
Cepheider i særdeleshed, er massive stjerner, med kort levetid, så de findes kun steder hvor der har været nylig stjernedannelse.
I elliptiske galakser er stjernedannelse normalt stoppet for længe siden og de har derfor ingen Cepheider.
I stedet må man bruge afstandsindikatorer, der stammer fra en ældre stjernepopulation (som novaer og RR Lyrae variable).
Men RR Lyrae variable er mindre lysstærke end Cepheider, og novaer er uforudsigelige og et intensivt overvågningsprogram – og held under overvågningen – er nødvendig for at samle nok novaer i målgalaksen til en god afstandsbedømmelse.
Fordi de mere fjerntliggende trin i den kosmiske afstandsstige afhænger af de tættere, indeholder de fjernere trin virkningerne af fejl i de tættere trin, både systematiske og tilfældige.
Resultatet af denne fejlophobning er, at afstande i astronomi sjældent er kendt med den samme nøjagtighed som i andre videnskaber, og at nøjagtigheden aftager med afstanden.
Et andet problem, specielt for de klareste standardlyskilder, er hvor ensartede de egentligt er i deres absolutte størrelsesklasse.
For en del af disse standardlyskilder udledes ensartetheden fra teorier om dannelse og udvikling af stjerner og galakser, og er derfor afhængig af nøjagtigheden i disse modeller.
For den mest lysstærke afstandsindikator Type Ia supernovaen, vides denne ensartethed at være ringe[27][bør uddybes].
Hubbles lov, den proportionale sammenhæng mellem afstand og fart for en galakse som fjerner sig fra os (normalt kaldet rødforskydning) er opstillet på baggrund af den kosmiske afstandsstige. Hubble observerede at svagere galakser er mere rødforskudt.
Bestemmelsen af Hubbles konstant var resultatet af årtiers arbejde af mange astronomer, både i indsamling af rødforskydningsdata og i kalibrering af afstandsstigen. Hubbles Lov er den primære metode til at anslå afstanden til kvasarer og fjerne galakser i hvilke individuelle afstandsindikatorer ikke kan ses.
Referencer[redigér | rediger kildetekst]
- ^ Ash, M.E., Shapiro, I.I., & Smith, W.B., 1967 Astronomical Journal, 72, 338–350.
- ^ Staff. "Trigonometric Parallax". The SAO Encyclopedia of Astronomy. Swinburne Centre for Astrophysics and Supercomputing. Hentet 2008-10-18.
- ^ Perryman, M. A. C.; et al. (1999). "The HIPPARCOS Catalogue". Astronomy and Astrophysics. 323: L49-L52. Bibcode:1997A&A...323L..49P.
- ^ Harrington, J.D.; Villard, Ray (10. april 2014). "NASA's Hubble Extends Stellar Tape Measure 10 Times Farther Into Space". NASA. Hentet 17. oktober 2014.
Riess, Adam G.; Casertano, Stefano; Anderson, Jay; Mackenty, John; Filippenko, Alexei V. "Parallax Beyond a Kiloparsec from Spatially Scanning the Wide Field Camera 3 on the Hubble Space Telescope". arXiv:1401.0484. Bibcode:2014ApJ...785..161R. doi:10.1088/0004-637X/785/2/161.
{{cite journal}}: Cite journal kræver|journal=(hjælp) - ^ Basu, Baidyanath (2003). An Introduction to Astrophysics. PHI Learning Private Limited. ISBN 81-203-1121-3.
- ^ Skabelon:Cite arXiv
- ^ Bartel, N., et al., 1994, "The shape, expansion rate and distance of supernova 1993J from VLBI measurements", Nature 368, 610–613
- ^ "Type Ia Supernova". Weekly Topic. Caglow. Arkiveret fra originalen 29. februar 2012. Hentet 30. januar 2012.
- ^ Linden, Sebastian; Virey, Jean-Marc; Tilquin, André (2009). "Cosmological parameter extraction and biases from type Ia supernova magnitude evolution". A&A. 506 (3): 1095-1105. arXiv:0907.4495. Bibcode:2009A&A...506.1095L. doi:10.1051/0004-6361/200912811., and references therein.
- ^ Bonanos, Alceste Z. (2006). "Eclipsing Binaries: Tools for Calibrating the Extragalactic Distance Scale". Binary Stars as Critical Tools and Tests in Contemporary Astrophysics, International Astronomical Union. Symposium no. 240, held 22–25 August 2006 in Prague, Czech Republic, S240, #008. 2: 79-87. arXiv:astro-ph/0610923. Bibcode:2007IAUS..240...79B. doi:10.1017/S1743921307003845.
- ^ Ferrarese, Laura; Ford, Holland C.; Huchra, John; Kennicutt, Robert C., Jr.; Mould, Jeremy R.; Sakai, Shoko; Freedman, Wendy L.; Stetson, Peter B.; Madore, Barry F.; Gibson, Brad K.; Graham, John A.; Hughes, Shaun M.; Illingworth, Garth D.; Kelson, Daniel D.; Macri, Lucas; Sebo, Kim; Silbermann, N. A.; Ford; Huchra; Kennicutt; Mould; Sakai; Freedman; Stetson; Madore; Gibson; Graham; Hughes; Illingworth; Kelson; Macri; Sebo; Silbermann (2000). "A Database of Cepheid Distance Moduli and Tip of the Red Giant Branch, Globular Cluster Luminosity Function, Planetary Nebula Luminosity Function, and Surface Brightness Fluctuation Data Useful for Distance Determinations". The Astrophysical Journal Supplement Series. 128 (2): 431-459. arXiv:astro-ph/9910501. Bibcode:2000ApJS..128..431F. doi:10.1086/313391.
{{cite journal}}: CS1-vedligeholdelse: Flere navne: authors list (link) - ^ S. A. Colgate (1979). "Supernovae as a standard candle for cosmology". Astrophysical Journal. 232 (1): 404-408. Bibcode:1979ApJ...232..404C. doi:10.1086/157300.
- ^ Adapted from Jacoby et al., Publ. Astron. Soc. Pac., 104, 499, 1992
- ^ Benedict, G. Fritz et al. "Hubble Space Telescope Fine Guidance Sensor Parallaxes of Galactic Cepheid Variable Stars: Period-Luminosity Relations", The Astronomical Journal, Volume 133, Issue 4, pp. 1810–1827 (2007)
- ^ Majaess, Daniel; Turner, David; Moni Bidin, Christian; Mauro, Francesco; Geisler, Douglas; Gieren, Wolfgang; Minniti, Dante; Chené, André-Nicolas; Lucas, Philip; Borissova, Jura; Kurtev, Radostn; Dékány, Istvan; Saito, Roberto K. "New Evidence Supporting Membership for TW Nor in Lyngå 6 and the Centaurus Spiral Arm", ApJ Letters, Volume 741, Issue 2, article id. L2 (2011)
- ^ Skabelon:Cite arXiv
- ^ Udalski, A.; Wyrzykowski, L.; Pietrzynski, G.; Szewczyk, O.; Szymanski, M.; Kubiak, M.; Soszynski, I.; Zebrun, K. (2001). "The Optical Gravitational Lensing Experiment. Cepheids in the Galaxy IC1613: No Dependence of the Period-Luminosity Relation on Metallicity". Acta Astronomica. 51: 221. arXiv:astro-ph/0109446. Bibcode:2001AcA....51..221U.
- ^ Ngeow, C.; Kanbur, S. M. (2006). "The Hubble Constant from Type Ia Supernovae Calibrated with the Linear and Nonlinear Cepheid Period-Luminosity Relations". The Astrophysical Journal. 642: L29. arXiv:astro-ph/0603643. Bibcode:2006ApJ...642L..29N. doi:10.1086/504478.
- ^ Macri, L. M.; Stanek, K. Z.; Bersier, D.; Greenhill, L. J.; Reid, M. J. (2006). "A New Cepheid Distance to the Maser–Host Galaxy NGC 4258 and Its Implications for the Hubble Constant". The Astrophysical Journal. 652 (2): 1133. arXiv:astro-ph/0608211. Bibcode:2006ApJ...652.1133M. doi:10.1086/508530.
- ^ Bono, G.; Caputo, F.; Fiorentino, G.; Marconi, M.; Musella, I. (2008). "Cepheids in External Galaxies. I. The Maser–Host Galaxy NGC 4258 and the Metallicity Dependence of Period–Luminosity and Period–Wesenheit Relations". The Astrophysical Journal. 684: 102. arXiv:0805.1592. Bibcode:2008ApJ...684..102B. doi:10.1086/589965.
- ^ Majaess, D.; Turner, D.; Lane, D. (2009). "Type II Cepheids as Extragalactic Distance Candles". Acta Astronomica. 59: 403. arXiv:0909.0181. Bibcode:2009AcA....59..403M.
- ^ Madore, Barry F.; Freedman, Wendy L. (2009). "Concerning the Slope of the Cepheid Period–Luminosity Relation". The Astrophysical Journal. 696 (2): 1498. arXiv:0902.3747. Bibcode:2009ApJ...696.1498M. doi:10.1088/0004-637X/696/2/1498.
- ^ Scowcroft, V.; Bersier, D.; Mould, J. R.; Wood, P. R. (2009). "The effect of metallicity on Cepheid magnitudes and the distance to M33". Monthly Notices of the Royal Astronomical Society. 396 (3): 1287. Bibcode:2009MNRAS.396.1287S. doi:10.1111/j.1365-2966.2009.14822.x.
- ^ Majaess, D. (2010). "The Cepheids of Centaurus A (NGC 5128) and Implications for H0". Acta Astronomica. 60: 121. arXiv:1006.2458. Bibcode:2010AcA....60..121M.
- ^ Tammann, G. A.; Sandage, A.; Reindl, B. (2008). "The expansion field: The value of H 0". Annual Review of Astronomy and Astrophysics. 15 (4): 289. arXiv:0806.3018. Bibcode:2008A&ARv..15..289T. doi:10.1007/s00159-008-0012-y.
- ^ Freedman, Wendy L.; Madore, Barry F. (2010). "The Hubble Constant". Annual Review of Astronomy and Astrophysics. 48: 673. arXiv:1004.1856. Bibcode:2010ARA&A..48..673F. doi:10.1146/annurev-astro-082708-101829.
- ^ Gilfanov, Marat; Bogdán, Ákos (2010). "An upper limit on the contribution of accreting white dwarfs to the type Ia supernova rate". Nature. 463 (3): 924-925. arXiv:1002.3359. Bibcode:2010Natur.463..924G. doi:10.1038/nature08685.
Bibliografi[redigér | rediger kildetekst]
- An Introduction to Modern Astrophysics, Carroll and Ostlie, copyright 2007.
- Measuring the Universe The Cosmological Distance Ladder, Stephen Webb, copyright 2001.
- Pasachoff, JM & Filippenko, AV, The Cosmos: Astronomy in the New Millennium, Cambridge: Cambridge University Press, 4th edition, 2013 ISBN 978-1-107-68756-1.
- The Astrophysical Journal, The Globular Cluster Luminosity Function as a Distance Indicator: Dynamical Effects, Ostriker and Gnedin, May 5, 1997.
- An Introduction to Distance Measurement in Astronomy, Richard de Grijs, Chichester: John Wiley & Sons, 2011, ISBN 978-0-470-51180-0.
Eksterne henvisninger[redigér | rediger kildetekst]
- The ABC's of distances (UCLA)
- The Extragalactic Distance Scale by Bill Keel
- The Hubble Space Telescope Key Project on the Extragalactic Distance Scale
- The Hubble Constant, a historical discussion
- NASA Cosmic Distance Scale
- PNLF information database Arkiveret 26. januar 2010 hos Wayback Machine
- The Astrophysical Journal













