Drejningsmoment: Forskelle mellem versioner
Inc (diskussion | bidrag) →Eksterne henvisninger: Linkfix Tags: Mobilredigering Mobilwebredigering Avanceret redigering fra mobil |
Inc (diskussion | bidrag) Tilføjet mere fysisk stringent afsnit deltvist kopieret fra Impulsmoment. Artiklen har dog generelt brug for at blive strammet op. Tag: 2017-kilderedigering |
||
| Linje 1: | Linje 1: | ||
{{Ingen kilder}} |
|||
'''Drejningsmoment''' (eller '''kraftmoment''') er et begreb fra den [[Klassisk mekanik|klassiske mekanik]], som beskriver en |
'''Drejningsmoment''' (eller '''kraftmoment''') er et begreb fra den [[Klassisk mekanik|klassiske mekanik]], som beskriver en [[kraft]]s påvirkning af et legeme i forhold til afstanden til et valgt punkt. Dette er et nyttigt koncept for at forstå roterende systemer lige fra Solsystemet til [[svensknøgle]]r. |
||
== Introduktion == |
|||
Jo længere væk fra aksen en bestemt kraft virker, desto større drejningsmoment har den. Drejningsmomentet er lig med kraft (''F'') gange arm (''L''), hvor arm er afstanden fra kraftens retningslinje til den akse legemet roterer omkring. Da drejningsmomentet ofte betegnes med det græske bogstav <math>\tau</math> (tau), kan definitionen på kraftmoment altså skrives |
Jo længere væk fra aksen en bestemt kraft virker, desto større drejningsmoment har den. Drejningsmomentet er lig med kraft (''F'') gange arm (''L''), hvor arm er afstanden fra kraftens retningslinje til den akse legemet roterer omkring. Da drejningsmomentet ofte betegnes med det græske bogstav <math>\tau</math> (tau), kan definitionen på kraftmoment altså skrives |
||
| Linje 16: | Linje 18: | ||
Den linje der går vinkelret gennem trækkraften <em>F</em>'s retning (ved nr. 3 på tegningen), og igennem omdrejningsaksen (1), kaldes for ''momentarmen'', og den vil altid være lige så lang som eller kortere end vægtstangens længde <em>L</em>. Når kraften <em>F</em> trækker "på skrå" i vægtstangen, skaber den samme drejningsmoment som et vinkelret træk med samme kraft ville gøre i den kortere momentarm. |
Den linje der går vinkelret gennem trækkraften <em>F</em>'s retning (ved nr. 3 på tegningen), og igennem omdrejningsaksen (1), kaldes for ''momentarmen'', og den vil altid være lige så lang som eller kortere end vægtstangens længde <em>L</em>. Når kraften <em>F</em> trækker "på skrå" i vægtstangen, skaber den samme drejningsmoment som et vinkelret træk med samme kraft ville gøre i den kortere momentarm. |
||
== Krafkmoment i klassisk mekanik == |
|||
Kraftmomentet er defineret ud fra [[impulsmoment]]et <math>\vec{L}</math>, der for en punktpartikel er givet ved: |
|||
{{Equation box 1 |
|||
|title= |
|||
|indent=: |
|||
|equation=<math>\vec{L} = \vec{r} \times \vec{p}</math> |
|||
|cellpadding = 6 |
|||
|border = 1 |
|||
|border colour = black |
|||
|background colour=white}} |
|||
hvor <math>\vec{r}</math> er [[stedvektor]]en for partiklens position regnet fra det valgte punkt, <math>\vec{p}</math> er partiklens [[Impuls (fysik)|impuls]] (impulsvektor), og produktet på højre side er et [[krydsprodukt]] af [[vektor (matematik)|vektorer]]. |
|||
Ligesom en lineær kraft <math>\vec{F}</math> er den afledte af impulsen med hensyn til tiden <math>t</math> |
|||
:<math>\vec{F} = \frac{d\vec{p}}{dt}</math> |
|||
er kraftmomentet <math>\vec{\tau}</math> defineret som den afledte af impulsmomentet i forhold til tiden: |
|||
{{Equation box 1 |
|||
|title= |
|||
|indent=: |
|||
|equation=<math>\vec{\tau} = \frac{d\vec{L}}{dt}</math> |
|||
|cellpadding = 6 |
|||
|border = 1 |
|||
|border colour = black |
|||
|background colour=white}} |
|||
hvor <math>t</math> er tid. |
|||
Ved at evaluere den [[differentialkvotient]]en med [[Regneregler for differentiation#Differentialkvotienten af produktet af to differentiable funktioner|produktreglen]], ses det, at: |
|||
:<math>\vec{\tau} = \frac{d\vec{r}}{dt} \times \vec{p}+\vec{r} \times \frac{d\vec{p}}{dt} =m(\vec{v} \times \vec{v})+\vec{r} \times \vec{F} </math> |
|||
Her er det brugt, at |
|||
:<math>\vec{p}=m\vec{v}</math> |
|||
hvor <math>m</math> er punktpartiklens masse, og <math>\vec{v}</math> er dens [[hastighed]]. Da krydsproduktet af en vektor med sig selv er nul, reducerer udtrykket for kraftmomentet til: |
|||
:<math>\vec{\tau} = \vec{r} \times \vec{F} </math> |
|||
Dette er i overestemmelse med kraftmomentet, som det er beskrevet tidligere i artiklen. |
|||
== Eksterne henvisninger == |
== Eksterne henvisninger == |
||
Versionen fra 19. okt. 2019, 17:50
Der er ingen kildehenvisninger i denne artikel, hvilket er et problem. (Lær hvordan og hvornår man kan fjerne denne skabelonbesked) |
Drejningsmoment (eller kraftmoment) er et begreb fra den klassiske mekanik, som beskriver en krafts påvirkning af et legeme i forhold til afstanden til et valgt punkt. Dette er et nyttigt koncept for at forstå roterende systemer lige fra Solsystemet til svensknøgler.
Introduktion
Jo længere væk fra aksen en bestemt kraft virker, desto større drejningsmoment har den. Drejningsmomentet er lig med kraft (F) gange arm (L), hvor arm er afstanden fra kraftens retningslinje til den akse legemet roterer omkring. Da drejningsmomentet ofte betegnes med det græske bogstav (tau), kan definitionen på kraftmoment altså skrives
Denne formel gælder kun når vinklen mellem kraftens retningslinje og armen er 90° For andre vinkler, se nedenfor. Anvender man eksempelvis en fastnøgle på en møtrik, bliver drejningsmomentet større jo mere kraft man bruger og jo længere ude på skaftet man holder.
Drejningsmomentet er for roterende bevægelser, hvad kraft er for legemer der bevæger sig lineært (translateres), f.eks. togvogne: Forøger man trækkraften, kan man få en togvogn (med konstant masse) til at accelerere hurtigere.
Analogt for roterende bevægelser vil et forøget drejningsmoment forøge vinkelaccelerationen for et legeme med konstant inertimoment; populært sagt får det større drejningsmoment det roterende legemes "omdrejningstal pr. minut" til at stige hurtigere.
Definition, dimension og måleenhed for drejningsmoment
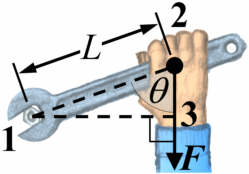
På tegningen til højre strammes en møtrik (1) med en fastnøgle, som derved fungerer som en vægtstang: Hånden griber om et punkt (2) i afstanden L fra møtrikken (dvs. omdrejningsaksen), og trækker i pilens retning med en kraft af størrelse F. Når vinklen mellem håndens trækkraft og vægtstangen (fastnøglens håndtag) er θ, er drejningsmomentet τ givet ved:
Heraf haves, at den fysiske dimension for drejningsmoment er kraft gange afstand, og SI-enheden for drejningsmoment bliver N·m (newton gange meter)
Den linje der går vinkelret gennem trækkraften F's retning (ved nr. 3 på tegningen), og igennem omdrejningsaksen (1), kaldes for momentarmen, og den vil altid være lige så lang som eller kortere end vægtstangens længde L. Når kraften F trækker "på skrå" i vægtstangen, skaber den samme drejningsmoment som et vinkelret træk med samme kraft ville gøre i den kortere momentarm.
Krafkmoment i klassisk mekanik
Kraftmomentet er defineret ud fra impulsmomentet , der for en punktpartikel er givet ved:
hvor er stedvektoren for partiklens position regnet fra det valgte punkt, er partiklens impuls (impulsvektor), og produktet på højre side er et krydsprodukt af vektorer.
Ligesom en lineær kraft er den afledte af impulsen med hensyn til tiden
er kraftmomentet defineret som den afledte af impulsmomentet i forhold til tiden:
hvor er tid.
Ved at evaluere den differentialkvotienten med produktreglen, ses det, at:
Her er det brugt, at
hvor er punktpartiklens masse, og er dens hastighed. Da krydsproduktet af en vektor med sig selv er nul, reducerer udtrykket for kraftmomentet til:
Dette er i overestemmelse med kraftmomentet, som det er beskrevet tidligere i artiklen.
Eksterne henvisninger
- Video fra Crash Course
- Video fra Khan Academy

















