Rødforskydning
| Fysisk kosmologi | ||||||||||||||
| Universet · Universets alder Big Bang · Tidslinje for Big Bang Observerbare univers Universets fremtid
| ||||||||||||||
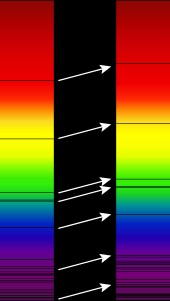
I fysikken (især astrofysikken), opstår fænomenet rødforskydning når lys, der ses kommende fra et objekt, er proportionalt forøget i bølgelængden, eller forskudt til den røde ende af spektret. Mere uddybet - hvor en observatør registrerer elektromagnetisk stråling udenfor det synlige spektrum, er "rødere" forskydning en teknisk forkortelse for "en stigning i elektromagnetismens bølgelængde" — som også indebærer lavere frekvens og fotonenergi i overensstemmelse med henholdsvis bølgeteorien og kvantumteorien for lys.
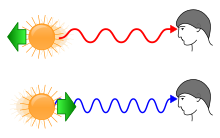
Populært kan man sige, at
- Hvis udsenderen og modtageren fjerner sig hinanden, bliver bølgerne trukket fra hinanden og bølgelængden bliver længere = rødforskydning
- Hvis udsenderen og modtageren nærmer sig hinanden bliver bølgerne presset sammen og bølgelængden bliver kortere = blåforskydning
Rødforskydning kan henføres til Dopplereffekten, der bedst kendes som forandringerne i den tilsyneladende tone af sirener og frekvensen af lydbølger, der udsendes af fremadkørende køretøjer. En observeret rødforskydning, på grund af Dopplereffekten, opstår når en lyskilde bevæger sig væk fra en observatør. Kosmologisk rødforskydning er set på grund af udvidelse af universet, og tilstrækkeligt fjerne lyskilder (generelt mere end få millioner lysår væk) har en rødforskydning svarende til stigningen af deres afstand fra Jorden. Endeligt er der rødforskydning forårsaget af tyngdekraft, det er en relativ effekt som observeres når elektromagnetisk stråling passerer ud af tyngdefelter. Modsat rødforskydning er et fald i bølgelængden, kaldet blåforskydning, generelt set når et lys-udsendende objekt bevæger sig mod en observatør. Eller når elektromagnetisk stråling bevæger sig ind i et såkaldt tyngdefelt.
Selvom observering af rødforskydning og blåforskydning har flere jordbaserede anvendelser (f.eks. Dopplerradar og radarkanoner),[1] er rødforskydning mest kendt fra de spektroskopiske observationer af astronomiske objekter.[2]
En speciel relativ rødforskydningsformel (og dens klassiske tilnærmelse) kan blive brugt til at udregne rødforskydningen af et nærliggende objekt, når rumtiden er flad. Dog har mange tilfælde af sorte huller og Big Bangs kosmologi krævet, at rødforskydningen bliver udregnet ved hjælp af den Generellle relativitetsteori.[3] Speciel relativ rødforskydning forårsaget af tyngdekraft, og kosmologisk rødforskydning kan forstås under referencerammen for transformationslovene. Der eksisterer andre fysiske processer, som kan lede til en forskydning af frekvensen af elektromagnetisk stråling. Deriblandt spredning og optiske effekter; dog, kan den resulterende forandring skelnes fra rigtig rødforskydning og er generelt ikke refereret som sådan.
Rødforskydningens formel[redigér | rediger kildetekst]
I den generelle relativitet kan man udlede flere formler, som er gældende for særlige tilfælde af rødforskydning i visse specielle rumtidsgeometrier, som opsummeres i den følgende tabel. I alle tilfælde er størrelsen af forskydningen (værdien af z) uafhængig af bølgelængden.[2]
| Rødforskydning type | Geometri | Formel[4] |
|---|---|---|
| Relativistisk Dopplereffekt | Minkowski-rum (flad rumtid) | for small for radial bevægelse. |
| Kosmologisk rødforskydning | FLRW rumtid (ekspanderende Big Bang univers) | |
| Rødforskydning forårsaget af tyngdekraft | alle i stationær rumtid (eller Schwarzschild's geometri) | (for Schwarzschild's geometri, |
Noter[redigér | rediger kildetekst]
- ^ Se Feynman, Leighton and Sands (1989) eller alle indledende bachelor (og mange højskoler) fysik tekstbøger. Se Taylor (1992) for en relativ diskussion.
- ^ a b Se Binney and Merrifeld (1998), Carroll and Ostlie (1996), Kutner (2003) for applikationer i astronomi.
- ^ Se Misner, Thorne and Wheeler (1973) and Weinberg (1971) eller nogle af fysisk kosmologi tekstbøger
- ^ Hvor z = rødforskydning; v|| = hastighed parallelt til sigtelinje (positivt hvis den bevæger sig væk fra modtageren); c = lysets hastighed; γ = Lorentzfaktoren; a = størrelses faktor; G = gravitationskonstanten; M = objektets masse; r = radiale Schwarzschild koordinat, gtt = t,t komponent af det metriske tensor








