Eulers formel
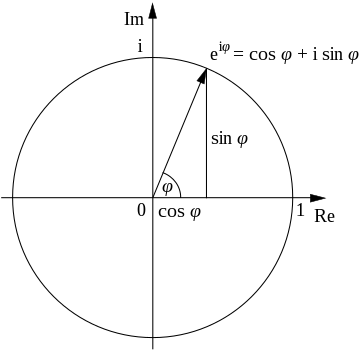
Eulers formel, opkaldt efter Leonhard Euler, er en matematisk formel i kompleks analyse, der viser en dyb relation mellem de trigonometriske funktion og den komplekse eksponentialfunktion.
Eulers formel siger at, der for alle reelle tal gælder, at
hvor
- er basen for den naturlige logaritme
- er den imaginære enhed.
- og er funktionerne sinus og cosinus.
Richard Feynman kaldte Eulers formel "vores ædelsten" og "den mest bemærkelsesværdige formel i matematikken." (Feynman, p. 22-10.)
Eulers identitet er et specialtilfælde af Eulers formel, hvor er :
Den blev ved en afstemning blandt matematikere i 1988 kåret som "den smukkeste formel i matematikken".[1] [2]
Historie[redigér | rediger kildetekst]
Eulers formel blev bevist (i en obskur form) for første gang af Roger Cotes i 1714, og siden hen genopdaget og gjort populær af Euler i 1748. Hverken Cotes eller Euler bemærkede den geometriske fortolkning af formlen: Idéen om de komplekse tal som punkter i planen opstod omtrent 50 år senere.
Anvendelser i kompleks talteori[redigér | rediger kildetekst]
Denne formel kan fortolkes på den måde, at funktionen eix løber på enhedscirklen i den komplekse plan, som x gennemløber de reelle tal. Her er x vinklen mellem den positive reelle akse og den linje, der forbinder origo med et punkt på enhedscirklen, målt mod uret og i radianer.
Beviset bygger på Taylorrækken for eksponentialfunktionen ez (hvor z er et komplekst tal) og for sin x og cos x for reelle tal x (se nedenfor.) Faktisk viser det samme bevis, at Eulers formel er gyldig for alle komplekse tal x.
Eulers formel kan bruges til at repræsentere komplekse tal i polære koordinater. Ethvert komplekst tal z = x + iy kan skrives som
hvor
- er modulus af z,
og er argumentet af z— vinklen mellem x-aksen og vektoren z målt mod uret og i radianer — defineret op til addition af 2π.
Med denne formel udledt, kan Eulers formel bruges til at definere logaritmen af et komplekst tal. For at gøre dette, bruges også de fakta, at
og
for alle komplekse tal a og b.
Derfor er det muligt at skrive:
for alle . At tage logaritmen på begge sider, viser at:
og dette kan bruges som definitionen på den komplekse logaritme. Logaritmen af et komplekst tal er dermed en funktion af flere værdier, da kan antage flere værdier.
Endelig medfører eksponentialloven
som kan vises at gælde for alle heltal k, sammen med Eulers formel, adskillige trigonometriske identiteter såvel som de Moivres formel.
Forbindelser med trigonometri[redigér | rediger kildetekst]
Eulers formel tilvejebringer en stærk forbindelse mellem analyse og trigonometri, og giver en fortolkning af sinus- og cosinusfunktionerne som vægtede summer af eksponentialfunktionen:
De to ovenstående ligninger kan udledes ved (hhv.) addition og subtraktion af Eulers formler:
og ved at løse med hensyn til enten sinus eller cosinus.
Disse formler kan endda tjene som definitioner på de trigonometriske funktioner med komplekse argumenter x. Ved at lade x = iy fås for eksempel, at:
Andre anvendelser[redigér | rediger kildetekst]
I differentialligninger bruges funktionen eix ofte at forenkle afledninger, selv hvis det endelige resultat er en reel funktion, der involverer sinus og cosinus. Eulers identitet følger let af Eulers formel.
I elektroteknik og andre områder, beskrives signaler, der ændrer sig periodisk over tid, som en kombination af sinus- og cosinusfunktioner (se Fourieranalyse,) og disse kan på belejlig vis udtrykkes som realdelen af eksponentialfunktionen med imaginære eksponenter, ved hjælp af Eulers formel.
Beviser[redigér | rediger kildetekst]
Ved brug af Taylorrækker[redigér | rediger kildetekst]
Her følger et bevis for Eulers formel ved brug af omtalte Taylorrækker såvel som grundlæggende fakta om potenser af i:
og så videre. Funktionerne ex, cos(x) og sin(x) kan, antagende at x er et reelt tal, skrives som:
og for komplekse z defineres hver af disse funktioner ved de ovenstående rækker, hvor x er erstattet med iz. Dette er muligt, da hver af rækkernes konvergensradius er uendelig. Det fås da, at
Omarrangeringen af leddene er tilladt, da hver af rækkerne konvergerer absolut. Ved at tage z = x til at være et reelt tal, fås den oprindelige identitet, som Euler opdagede den.
Ved brug af infinitesimalregning[redigér | rediger kildetekst]
Lad være en funktion defineret ved
Dette er tilladt, da
medfører, at aldrig er nul.
Den afledte af er, ifølge kvotientregelen:
Derfor må være en konstant funktion, og af
fås, at konstanten må være 1. Derfor må tæller og nævner i definitionen af være lig hinanden for alle , men det er netop Eulers formel.
Se også[redigér | rediger kildetekst]
Referencer[redigér | rediger kildetekst]
- Feynman, Richard P., The Feynman Lectures on Physics, vol. I Addison-Wesley (1977), ISBN 0-201-02010-6, ISBN 0-201-02116-1
- ^ David Wells: Which is the most beautiful?. Mathematical Intelligencer. 10, (4), side 30 – 31, 1988. doi:10.1007/BF03023741.
- ^ David Wells: Are these the most beautiful?. Mathematical Intelligencer. 12, (3), side 37 – 41, 1990. doi:10.1007/BF03024015.











































![{\displaystyle {\begin{matrix}f'(x)&=&\displaystyle {\frac {(-\sin x+i\cos x)\cdot e^{ix}-(\cos x+i\sin x)\cdot i\cdot e^{ix}}{(e^{ix})^{2}}}\\[1em]&=&\displaystyle {\frac {-\sin x\cdot e^{ix}-i^{2}\sin x\cdot e^{ix}}{(e^{ix})^{2}}}\\[1em]&=&0.\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b91d5d7376c12c42e52af18f42a9b77dbfb03fc8)
