Vektor (geometri)

"vektor" omdirigeres hertil. For andre betydninger af vektor, se vektor (flertydig).

Denne artikel bør gennemlæses af en person med fagkendskab for at sikre den faglige korrekthed.

En vektor er i geometrien et objekt, der er defineret ved at have en længde og en retning. To vektorer regnes for at være ens, hvis de har samme længde og retning, også selvom de er placeret forskellige steder. Vektorer kan dermed parallelforskydes. Vektorer der udgår fra et koordinatsystems origo (0,0,..) kaldes stedvektorer. En vektor kan opfattes som et orienteret liniestykke; Med andre ord: En vektor kan forstås som et linjestykke med retningsangivelse. I modsætning til vektorer kaldes normale tal, som kun har én størrelse (én dimension) og ingen retning, for skalarer. En vektor, som ikke er en stedvektor, kaldes en egentlig vektor.

Vektorer anvendes også i andre sammenhænge end geometri, hvor et fænomen defineres ved både størrelse og retning, for eksempel til at beskrive hastigheder. En hastighed har nemlig både en størrelse (kaldet farten) og en retning. Inden for fysikken beskriver vektorer også eksempelvis kræfter og acceleration etc. Vektorer anvendes ofte i to dimensioner (en plan), eller i tre dimensioner (rummet), men vektorer kan anvendes i ethvert antal dimensioner - endda uendeligt mange (abstrakte) dimensioner. Nul-vektoren har samme dimension som det rum, den er i og kan skrives 0. Den er atypisk, fordi den i modsætning til de øvrige (såkaldte egentlige) vektorer ingen retning/udstrækning har.

Notation

Vektorer skrives ofte med en pil over et lille bogstav, men andre notationer ses også. Samtlige nedenstående måder at repræsentere en vektor på forekommer.

${\vec {a}},{\overline {a}},{\underline {a}},\mathbf {a}$

Hvis en vektor er defineret ud fra liniestykke, der udgår fra punkt A og ender i punkt B, benyttes skrivemåden ${\overrightarrow {AB}}$, idet retningen bestemmes af udgangs- og slutpunktet. Vektoren ${\overrightarrow {AA}}={\vec {0}}$ definerer ethvert enkelt punkt, da et punkt pr. definition ingen udstrækning har.

Hvis man for eksempel i to dimensioner har en vektor med længden 5 og vinklen 45 grader i forhold til vandret (x- eller førsteaksen), kan man skrive:

${\vec {a}}=5\angle 45^{\circ }$

Skrivemåden anvendes mest ved repræsentation af komplekse tal med en vektor.

Ellers angives en vektor i matrixform - enten som en søjle (kolonne):

${\vec {a}}={a_{1} \choose a_{2}}$

eller række af vektorkoordinater: ${\vec {a}}=[a_{1},a_{2}]$ eller $(a_{1},a_{2})$.

Hvis en vektors længde og vinkel er givet, og man ønsker at omskrive den til matrix-form, kan det gøres det sådan:

${\vec {a}}=L\angle v$

${\vec {a}}={L\cdot \cos v \choose L\cdot \sin v}$

En vektor i tre eller flere dimensioner repræsenteres på lignende vis - blot med tilføjelse af en eller flere ekstra koordinater:

${\vec {a}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}$

Vektor i n dimensioner, når n er et naturligt tal:

${\vec {a}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\\\vdots \\a_{n}\end{pmatrix}}$

Længde af vektorer

Længden af en vektor kan beregnes vha. Pythagoras, da man faktisk kan opfatte en vektor som hypotenusen i en retvinklet trekant, hvis kateters længder angives af vektorens koordinater. En vektors længde betegnes med ||·|| eller |.| og bestemmes sådan:

$\|{\vec {a}}\|$

Formlen for længden af en én-dimensional vektor (en såkaldt Skalar) er givet ved:

$\|{\vec {a}}\|={\sqrt {{\vec {a}}\cdot {\vec {a}}}}={\sqrt {a_{1}^{2}}}$ , for ${\vec {a}}\ ={\begin{pmatrix}a_{1}\end{pmatrix}}$

Formlen for længden af en to-dimensional vektor er givet ved:

$\|{\vec {a}}\|={\sqrt {{\vec {a}}\cdot {\vec {a}}}}={\sqrt {a_{1}^{2}+a_{2}^{2}}}$ , for ${\vec {a}}\ ={\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}$

Formlen for længden af en n-dimensional vektor er givet ved:

$\|{\vec {a}}\|={\sqrt {{\vec {a}}\cdot {\vec {a}}}}={\sqrt {a_{1}^{2}+a_{2}^{2}...+a_{n}^{2}}}$ , for ${\vec {a}}\ ={\begin{pmatrix}a_{1}\\a_{2}\\\vdots \\a_{n}\end{pmatrix}}$

Prikken under kvadratrodstegnet i det såkaldte prikprodukt er ikke et (almindeligt) gangetegn, som man ellers let kunne tro. Se eventuelt definitionen af prikproduktet længere nede. At der er tale om priknotation og ikke normal multiplikation, er som regel underforstået, når prikken står mellem to vektorer. Bemærk, at en vektor ikke kan have en negativ længde. Prikproduktet kaldes også for skalarproduktet af to vektorer, fordi resultatet er en skalar. En vektor, som har længden 1 kaldes enhedsvektor.

Addition af vektorer

Addition af vektorer

Når man skal lægge to vektorer sammen (med henblik på at finde en resulterende kraft), får man en ny vektor, den såkaldte sumvektor. Her benævnt med ${\vec {r}}$. Hvis man har to vektorer i det samme to-dimensionale rum:

${\vec {a}}={a_{1} \choose a_{2}}$ og ${\vec {b}}={b_{1} \choose b_{2}}$,

lægges de sammen på følgende måde:

${\vec {r}}={a_{1}+b_{1} \choose a_{2}+b_{2}}$

Hvis man har tre eller flere vektorer, lægges de sammen efter samme princip: alle første-koordinaterne adderes, og alle anden-koordinaterne adderes etc. Summation af to vektorer kan foretages grafisk ved at placere den sidste vektors startpunkt, hvor den første har sit slutpunkt.

Subtraktion af vektorer

Subtraktion af vektorer

Vektorer trækkes fra hinanden, efter samme princip, som man lægger sammen. Dog kan man opfatte vektorers differens som:

${\vec {a}}+(-{\vec {b}})$

At man skriver $-{\vec {b}}$ betyder simpelthen at vektoren vendes og går i den modsatte retning. Det opfattes også som:

$(-{\vec {b}})={-b_{1} \choose -b_{2}}$

Men dette bruges kun grafisk. Analytisk trækker man vektorer fra hinanden:

${\vec {r}}={a_{1}-b_{1} \choose a_{2}-b_{2}}$

Grundet lighederne med addition, er principperne ligeledes de samme for vektorer af vilkårlig dimension.

Skalering af vektor

Når man skalerer en vektors, ganger man hver af vektorens koordinater med skaleringsfaktoren. Formlen er for vektorer i to dimensioner givet ved:

$x\cdot {\vec {a}}={x\cdot a_{1} \choose x\cdot a_{2}}$

Man kalder også dette for skalarmultiplikation af en vektor. Skalaren $x$ ganges altså på hver af koordinaterne i vektoren. Her til højre ses to tilfælde, når henholdsvis $x=2$ og $x=-1$. Bemærk dog at regnereglen gør sig gældende for alle reelle tal, og ikke blot for heltal. Samme formel benyttes for vektorer i n dimensioner.

Når skalaren $x$ er ganget på vektoren ${\vec {a}}$ vil vektoren nu have længden $|x|\cdot \|{\vec {a}}\|$. Herudover vil vinklen i forhold til $x$-aksen være bevaret, såfremt $x$ er positiv. I tilfælde af at $x$ skulle være negativ, vil vinklen være drejet 180 grader.

Tværvektor

Tværvektoren er den vektor der står vinkelret på ${\vec {a}}$ drejet mod urets retning. Denne bliver undertiden også kaldet for hat-vektoren, da den noteres som ${\hat {a}}$. Tværvektoren er kun defineret for vektorer i planen, da der i vektorrum med højere dimension end to findes uendelig mange drejede vektorer, der står vinkelret på den oprindelige vektor.

Det er let at overbevise sig selv om at tværvektoren til en vektor ${\vec {a}}={x \choose y}$ er givet ved ${\hat {a}}={-y \choose x}$.

Prikprodukt

Uddybende artikel: Skalarprodukt

De respektive informationer til skalarproduktet af to vektorer

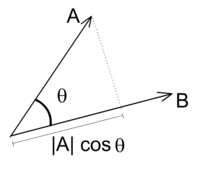
Prikproduktet (også kaldet skalarproduktet) er defineret for n-dimensionale vektorer og er en skalar. Prikproduktet noteres ofte med en prik: $\cdot$, som ikke må forveksles med et gangetegn, men da to vektorer sjældent kan ganges sammen er der imidlertid ikke noget at tage fejl af. Nogle steder i litteraturen er prikken dog gjort ekstra stor, så der slet ikke er nogen tvivl om hvad der menes. Prikproduktet kaldes også for det indre produkt. For det n-dimensionelle tilfælde ser prikproduktet ud på denne måde:

${\vec {a}}\bullet {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\\vdots \\a_{n}\end{pmatrix}}\bullet {\begin{pmatrix}b_{1}\\b_{2}\\\vdots \\b_{n}\end{pmatrix}}=\sum _{i=1}^{n}a_{i}\cdot b_{i}=a_{1}\cdot b_{1}+a_{2}\cdot b_{2}+\cdots +a_{n}\cdot b_{n}$

Resultatet af prikproduktet altså et tal! For geometriske vektorerer gælder der ydermere at prikproduktet har følgende egenskab:

${\vec {a}}\bullet {\vec {b}}=\|a\|\cdot \|b\|\cdot \cos \theta$

Regneregler for prikproduktet:

Givet tre vektorer a, b og c i planen eller rummet, samt tallet k. Der gælder:

$\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a}$ (kommutativ regel)

$\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c}$ (distributiv regel)

$(k\mathbf {a} )\cdot \mathbf {b} =\mathbf {a} \cdot (k\mathbf {b} )=k(\mathbf {a} \cdot \mathbf {b} )$

$\mathbf {a} \cdot \mathbf {a} =|\mathbf {a} |^{2}$

$|\mathbf {a} +\mathbf {b} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}+2\mathbf {a} \cdot \mathbf {b}$

Projektioner:

Givet to egentlige vektorer a og b i planen eller rummet så er længden af den ortogonale projektionen af b på a

$|Proj(\mathbf {b} ,\mathbf {a} )|={\frac {|\mathbf {a} \cdot \mathbf {b} |}{|\mathbf {a} |}}$ og projektions vektoren:

$Proj(\mathbf {b} ,\mathbf {a} )={\frac {|\mathbf {a} \cdot \mathbf {b} |}{|\mathbf {a} |^{2}}}\mathbf {a}$

Planprodukt

Uddybende artikel: Planprodukt

Planproduktet er udelukkende defineret for to-dimensionale vektorer og er lig med en skalar, hvis numeriske værdi er arealet af det parallelogram, der udspændes af to vektorer. Fortegnet angiver, om de to vektorer er positivt orienterede eller negativt orienterede. Planproduktet er determinanten af den matrix der opstår ved at sammensætte søjle vektorernes koordinater i en matrix. Formlen for planproduktet af to vektorer er angivet nedenfor. Det kan kaldes et skalarprodukt, men dette kan dog forveksles med prikproduktet.

$\det([{\vec {a}}{\vec {b}}])=\det({\begin{bmatrix}a_{1}&b_{1}\\a_{2}&b_{2}\end{bmatrix}})=a_{1}b_{2}-a_{2}b_{1}.$

Hvis de to vektorer udgår fra samme punkt P og således danner to sider af en trekant så er det halve planprodukt lig med arealet af trekanten.

Planprodukt og prikprodukt er relaterede ved formlerne

$\det([{\vec {a}}{\vec {b}}])={\hat {a}}\bullet {\vec {b}}$

og

${\vec {a}}\bullet {\vec {b}}=\det([{\vec {a}}{\hat {b}}]).$

Krydsprodukt

Uddybende artikel: Krydsprodukt

Krydsprodukt

Krydsproduktet er udelukkende defineret for tre-dimensionale vektorer og er lig med en vektor, der står vinkelret på den plan, der udspændes af to vektorer. Krydsproduktet noteres med et kryds: ×. Den måde, hvorpå krydsproduktet udregnes, kræver beregning af hele tre determinanter. "Formlen" for krydsproduktet imellem to vektorer er angivet nedenfor.

${\vec {a}}\times {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\times {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}\det {\begin{pmatrix}a_{2}&b_{2}\\a_{3}&b_{3}\end{pmatrix}}\\\det {\begin{pmatrix}a_{3}&b_{3}\\a_{1}&b_{1}\end{pmatrix}}\\\det {\begin{pmatrix}a_{1}&b_{1}\\a_{2}&b_{2}\end{pmatrix}}\end{pmatrix}}={\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{pmatrix}}$

Bemærk at krydsproduktet giver en vektor som resultat og at resultat vektoren ikke ligger i samme plan som de to vektorer der danner krydsproduktet. Herudover har denne nye vektor også den egenskab at dens længde angiver arealet af det parallelogram som de to vektorer udspænder. Til sidst kan størrelsen af krydsproduktet også benyttes til at bestemme vinklen imellem de to vektorer.

$\|{\vec {a}}\times {\vec {b}}\|=\|{\vec {a}}\|\cdot \|{\vec {b}}\|\cdot \sin \theta$.

Man skal bemærke at :

${\vec {a}}\times {\vec {b}}=-{\vec {b}}\times {\vec {a}}$

Mere formelt

Vinkler mellem Vektorer

Ved vinklen mellem to egentlige vektorer i planen forstår man den entydigt bestemte vinkel mellem deres stedvektorer (deres repræsentanter med samme startpunkt, nemlig udgående fra origo ), som ligger i intervallet [0; 2 π ] . Hvis en vektor u i planen drejes vinklen π/2 mod uret, fremkommer en ny vektor, der kaldes u's tværvektor og betegnes û. Ved vinklen mellem to egentlige vektorer i rummet forstås vinklen mellem deres stedvektorer i den plan i rummet, som indeholder begge stedvektorer når de er placeret med origo som udgangspunkt.

Multiplikation med skalar

Der er givet en vektor v i planen eller rummet (evt med mere end 3 dimensioner) og en skalar k. Hvis v=0 , sætter vi kv = vk =0. I modsat fald forstås der ved produktet kv følgende:

• Hvis k>0 så er kv = vk den vektor, der har samme retning som v , men som er gange k så lang som v .
• Hvis k=0 så er kv =0
• Hvis k<0 så er kv = vk den vektor der har modsat retning af v , og som er |k| gange så lang som v.

Man ser at multiplicerer vi v med -1 så får vi en modsat rettet vektor (-1) v = -v .

Nul reglen for geometriske vektorer er $k\mathbf {v} =0\Leftrightarrow k=0\;\;eller\;\;\mathbf {v} =0$ i ord, hvis k v =0 så er entern k eller v lig nul og omvendt hvis enten k eller v eller begge er nul så er k v =0;

Parameterfremstilling

Der er givet en ret linje , som går gennem origo O. Punkterne på linjen beskrives ved hjælp af en parameterfremstilling.

Der vælges et punkt P på en linje , der ikke er det samme som origo. Vektoren $\mathbf {r} ={\vec {OP}}$ kaldes en retningsvektor for linjen . Til ethvert punkt linjen på svarer der netop ét reelt tal t, der opfylder, at ${\vec {OP}}=t\mathbf {r}$. Omvendt svarer der til ethvert tal t netop ét punkt P på linjen , så ${\vec {OP}}=t\mathbf {r}$ . Når t gennemløber de reelle tal fra $-\infty \;\;til\;\;+\infty$ , vil P gennemløbe hele linjen i den retning, som er bestemt ved r . Man siger, at

$\{P|{\vec {OP}}=t\mathbf {r} \;\;hvor\;\;t\in \mathbb {R} \}$

er en parameter fremstilling af linjen. Det fremhævede R er mængden af de reelle tall.

Givet en linje , der ikke går gennem origo. Punkterne P på linjen beskrives ved hjælp af en parameterfremstilling.

Først vælges et begyndelsespunkt B på linjen, vektoren b sættes til vektoren ${\vec {OB}}$ .Vektoren $\mathbf {r} ={\vec {BP}}$ er da en retningsvektor for linjen. Til ethvert punkt på linjen svarer der netop ét reelt tal t , der opfylder, at ${\vec {OP}}=\mathbf {b} +t\mathbf {r}$ . Omvendt svarer der til ethvert tal t netop ét punkt P på linjen , så ${\vec {OP}}=\mathbf {b} +t\mathbf {r}$ . Når t gennemløber de reelle tal fra $-\infty \;\;til\;\;+\infty$ , vil P gennemløbe hele linjen i den retning, som er bestemt ved r . Man siger, at

$\{P|{\vec {OP}}=\mathbf {b} +t\mathbf {r} \;\;hvor\;\;t\in \mathbb {R} \}$

er en parameter fremstilling af linjen.

Parameterfremstillinger som ovenfor beskriver rette linjer, der er uendeligt lange i hver retning. Men parameterfremstillinger kan afgrænses og derved også bruges til at beskrive linjestykker, her liniestykket hvor parameteren t begrænses til intervallet fra (-2) til 5 .

$\{P|{\vec {OP}}=\mathbf {b} +t\mathbf {r} \;\;hvor\;\;t\in [-2;5]\}$

Regneregler

Det er vigtigt at bestemme regnereglerne for vektorer mere eksakt. Derved bliver en struktur defineret som kan anvendes for andre ting man kunne tænke sig at behandle nøjagtigt som vektorer. Er strukturerne ens så ligner de andre ting vektorer i den betydning at man kan udføre de samme operationer med dem.

For vilkårlige geometriske vektorer u, v og w og for vilkårlige reelle tal k og k₁ og k₂ gælder følgende regneregler:

• u+v = v+u ; Addition er kommutativ
• (u+v) + w = u+ (v+w); Addition er associativ
• u+0 = u; Nulvektoren er neutral ved addition
• u+ (-u) = 0 ; Summen af en vektor og dens modsatte er nul
• k₁ (k₂u) = (k₁ k₂) u ; Multiplikation af vektor med skalar er associativ
• (k₁ + k₂) u = k₁ u + k₂u Distributiv regel
• k (u+v) = k u+ k v; Distributiv regel
• 1 u = u ; Skalaren 1 er neutral i produkt med vektorer

Det skal også forstås at disse operationer på geometriske vektorer frembringer nye geometriske vektorer og at vektorerne bliver i det rum de er skabt i. Det kaldes at operationerne er stabile med hensyn til vektorernes rum. Prøv at tegne disse definitioner grafisk.

Man skal bemærke at der ikke er defineret et vektor produkt.

Linearkombinationer

Når der er givet reelle tal k₁ , k ₂, k₃, ..., k _n og vektorerne v₁ , v ₂, v₃, ..., v _n, så kaldes summen

$\mathbf {v} =k_{1}\mathbf {v} _{1}+k_{2}\mathbf {v} _{2}+k_{3}\mathbf {v} _{3}+\cdots k_{n}\mathbf {v} _{n}$

en linearkombination af de givne vektorer

Hvis alle koefficienterne k _j er lig med 0, kaldes linearkombinationen uegentlig. Men hvis blot én af dem er forskellig fra 0, er den egentlig.

Lineær afhængighed og lineær uafhængighed

Hvis to vektorer har repræsentanter på den samme rette linje, siger man, at de er lineært afhængige. Det er klart, at to egentlige vektorer er lineært afhængige, hvis de er parallelle. I modsat fald er de lineært uafhængige. Vi kan formulere det således, at to vektorer u og v er lineært afhængige, hvis den ene kan fremkomme af den anden ved multiplikation med en skalar forskellig fra nul , dvs. hvis der findes et tal k≠0 således, at

$\mathbf {v} =k\mathbf {u}$

Kort sagt, to vektorer er lineært afhængige, ”`hvis den ene kan beskrive den anden”'. To parallelle vektorer kan beskrive hinanden ved, at den ene kopieres og lægges til (eller trækkes fra) sig selv et vist antal gange; altså, ved at den forlænges eller forkortes.

To vinkelrette eller blot ikke-parallelle vektorer kan derimod aldrig beskrive hinanden, uanset hvor meget vi forlænger eller forkorter dem, da vi er nødt til at dreje den ene, før det bliver muligt. Disse er derfor lineært uafhængige.

Denne oprindelige betydning af begreberne lineær afhængighed og uafhængighed ønsker vi at generalisere sådan, at begreberne kan bruges om et vilkårligt sæt af vektorer.

Et sæt af vektorer v₁ , v ₂, v₃, ..., v _n , hvor n≥2 kaldes lineært afhængigt, hvis mindst én af vektorerne kan skrives som en linearkombination af de øvrige.

Hvis ingen af vektorerne kan skrives som en linearkombination af de øvrige, kaldes sættet for lineært uafhængigt.

Et sæt, som kun består af én vektor, kaldes lineært afhængigt, hvis vektoren er 0-vektoren, og ellers lineært uafhængigt.

Mere formelt

Lad k _j være reelle tal. At vektorsættet v₁ , v ₂, v, ..., v _n er lineært uafhængigt, er ensbetydende med, at ligningen

$k_{1}\mathbf {v} _{1}+k_{2}\mathbf {v} _{2}+\cdots k_{n}\mathbf {v} _{n}=\mathbf {0}$

kun er opfyldt, når alle koefficienterne er lig med 0.

Eksempel: Sættet (a,b,c ) er lineært afhængigt hvis $k_{a}\mathbf {a} +k_{b}\mathbf {b} +k_{c}\mathbf {c} =\mathbf {0}$ dvs en vilkårlig af vektorerne kan udstykkes ved de to andre. Hvis de tre vektorer er i det tredimensionale rum må de nødvendigvis ligge i samme plan. På den anden side hvis tre vektorer ligger i samme plan så er de lineært afhængige. Dette er ensbetydende med at en plan kan frembringes ved en parameter fremstilling helt i linje med en parameterfremstilling for en linje fx:

$\{P|{\vec {OP}}=\mathbf {b} +r\mathbf {u} +s\mathbf {v} \;\;hvor\;\;(r,s)\in \mathbb {R} \}$

r og s er parametrene og b er vektoren fra Origo til et vilkårligt punkt i planen

De sædvanlige baser i planen og rummet

I den analytiske geometri (opfundet af Rene Decarte (1596-1650) som også opfandt kordinatsystemet) viser man, hvordan tal og ligninger kan beskrive geometriske objekter og fænomener herunder vektorer. Her er begrebet koordinater afgørende. Det handler nemlig om, hvordan vi kan fastlægge de geometriske objekters placering i rummet og i forhold til hinanden ved hjælp af tal og talsæt.

For at få grundlaget i orden skal vi vælge et vist antal vektorer, som vi udnævner til basisvektorer. Basisvektorer er vektorer, der ved hinandens hjælp udspænder et rum fuldstændigt (fx et 2D- eller 3D-rum), forstået på den måde at de kan beskrive alle andre vektorer i dette rum. Basisvektorerne ordnes — dvs. arrangeres i en bestemt rækkefølge — og udgør herefter en basis for det pågældende rum. Når en basis er givet, kan samtlige vektorer, der overhovedet er mulige at generere i det pågældende rum, beskrives ved hjælp af koordinater, som er basisvektorernes koefficienter, og koordinaterne samler vi som regel i såkaldte koordinatvektorer.

Hvordan hele denne procedure foregår, udfolder vi først gennem standardbaserne i planen og rummet. Senere kommer vi ind på, at det ofte kan være hensigtsmæssigt at benytte andre baser end de sædvanlige, og på hvordan relationen mellem en vektors koordinater er i forskellige baser.

Standardbasis i planen

Ved en standardbasis eller sædvanlig basis for de geometriske vektorer i planen forstås et ordnet sæt af to vektorer (i,j) , som opfylder:

$\mathbf {i}$ har længden 1, og $\mathbf {j} =\mathbf {\hat {i}}$ .

(det vil sige, j er tværvektor for i ).

Ved et sædvanligt koordinatsystem i planen forstås en standardbasis (i,j) sammen med et valgt origo O. Koordinatsystemet skrives ( O, i,j) Ved x-aksen og y-aksen forstås orienterede tallinjer gennem O , som er parallelle med henholdsvis i og j.

En vektors koordinater

Hvis e = (i,j) er en standardbasis, kan enhver vektor v i planen på netop én måde skrives som en linearkombination af i og j:

$\mathbf {v} =x\mathbf {i} +y\mathbf {j}$

Koefficienterne x og y i linearkombinationen kaldes v's koordinater med hensyn til basen e, eller kortere: v's e-koordinater, og de samles i en koordinatvektor med følgende skrivemåde:

${}_{e}\mathbf {v} ={\begin{bmatrix}x\\y\end{bmatrix}}$

Man giver normalt standard basen navnet e.

Et punkts koordinater

Lad P være et vilkårligt punkt i planen, og lad (O,i,j) være et sædvanligt koordinatsystem i planen. Ved koordinaterne for P med hensyn til koordinatsystemet forstås koordinaterne for stedvektoren ${\vec {OP}}$ med hensyn til standardbasen (i,j) .

Vektorregning i regneark

Noget vektorregning kan klares ved at indtaste formler i regneark som f.eks. Microsoft Excel:

Bl.a. at beregne vektors længde samt vektoraddition og vektorsubtraktion; endelig kan også skalarprodukt og vektorproduktets koordinater beregnes af formler, som man indtaster i regneark. Det gælder for vektorer i planen (2D) og for vektorer i rummet (3D).

Matematisk software så som Maple kan også regne med vektorer. Grafregneren TI-89 kan beregne krydsprodukt.

Bøger

• Holth, Klaus m.fl. (1987): Matematik Grundbog 1. Forlaget Trip, Vejle. ISBN 87-88049-18-3
• Schultz, Jonny (1990): Matematik Højniveau 1. Forlaget Trip, Vejle. ISBN 87-88049-16-7

Noter

• Wikimedia Commons har flere filer relateret til Vektor (geometri)