Matematik





Matematik (fra oldgræsk μάθημα; máthēma: 'viden, læring, studie') er et vidensområde, der omfatter emner som tal (aritmetik og talteori),[1] formler og relaterede strukturer (algebra),[2] former og rummene, hvori de er indesluttet (geometri),[1] og mængder og deres ændringer (kalkulus og analyse).[3][4][5] De fleste matematiske aktiviteter involverer brugen af ren fornuft til at opdage eller bevise egenskaberne ved abstrakte objekter, som består af enten abstraktioner fra naturen eller – i moderne matematik – enheder, der er fastsat med bestemte egenskaber, kaldet aksiomer. Et matematisk bevis består af en række anvendelser af nogle deduktive regler på allerede kendte resultater, herunder tidligere beviste teoremer, aksiomer og (i tilfælde af abstraktion fra naturen) nogle grundlæggende egenskaber, som betragtes som sande udgangspunkter for teorien i betragtning.
Matematik bruges i videnskaben til modelopsætning af fænomener, som så tillader forudsigelser at blive lavet ud fra eksperimentelle love. Den matematiske sandheds uafhængighed af enhver eksperimentering indebærer, at nøjagtigheden af sådanne forudsigelser kun afhænger af modellens tilstrækkelighed. Upræcise forudsigelser, snarere end at være forårsaget af forkert matematik, indebærer behovet for at ændre den anvendte matematiske model. For eksempel kunne Merkurs perihelion-præcession først forklares efter fremkomsten af Einsteins generelle relativitetsteori, som erstattede Newtons tyngdelov som en bedre matematisk model.
Matematik er essentielt inden for videnskab, iværksætteri, lægemidler, finans, datalogi og samfundsvidenskab. Nogle områder af matematik, såsom statistik og spilteori, er udviklet i tæt korrelation med deres anvendelser og er ofte grupperet under anvendt matematik. Andre matematikområder udvikles uafhængigt af enhver applikation (og kaldes derfor ren matematik), men praktiske applikationer opdages ofte senere. Et passende eksempel er problemet med heltalsfaktorisering, som går tilbage til Euklid, men som ikke havde nogen praktisk anvendelse før den blev brugt i RSA-kryptosystemet (til computernetværkssikkerhed).
Historisk dukkede konceptet om et bevis og dets tilhørende matematiske stringens først op i græsk matematik, især i Euklids Elementerne.[6] Siden begyndelsen var matematik i det væsentlige opdelt i geometri og aritmetik (manipulation af naturlige tal og brøker), indtil det 16. og 17. århundrede, hvor algebra[a] og infinitesimalkalkulus blev introduceret som nye områder af emnet. Siden da har samspillet mellem matematiske innovationer og videnskabelige opdagelser ført til en hurtig stigning i udviklingen af matematik. I slutningen af det 19. århundrede førte matematikkens grundlæggende krise til systematiseringen af den aksiomatiske metode. Dette gav anledning til en dramatisk stigning i antallet af matematikområder og deres anvendelsesområder. Et eksempel på dette er Matematikfagsklassifikationen, som oplister mere end 60 matematikområder på første niveau.
Definition
[redigér | rediger kildetekst]Matematik er et fag, der har eksisteret i 5.000 år, det har ry for at være tørt og kedeligt, svært og utilgængeligt, abstrakt, virkeligheds- og menneskefjernt, ja nogle vil måske endda mene menneskefjendsk.
Matematikere er en slags franskmænd: snakker du med dem, oversætter de til deres eget sprog, og så er det straks noget helt andet.
Mit det sværeste i skolen er regning, og det som er det sværeste i regning, er at få det til at blive det, det skal!
Matematikken er en deduktiv og abstrakt videnskab, som bygger på logiske metoder. I den moderne definition er det undersøgelsen af aksiomatisk definerede abstrakte strukturer ved brug af logik, læren om sandt og falsk, som er det fælles udgangspunkt.[kilde mangler] De specifikke strukturer, der undersøges, har ofte deres udgangspunkt i naturvidenskaben, oftest i fysikken. Men i modsætning til naturvidenskaben beskriver matematikken en uvirkelig ideel verden, hvor for eksempel rette eller parallelle linjer findes modsat den virkelige verden. Matematikere definerer og undersøger også strukturer udelukkende af hensyn til matematikkens udvikling af egne regler, for eksempel fordi de finder ud af, at en struktur giver en samlende generalisering, eller at der findes et værktøj, der kan hjælpe i flere forskellige grene af matematikken.[kilde mangler]
Der findes dog ikke nogen alment accepteret definition på, hvad matematik er.[10][11] Aristoteles definerede faget som "videnskaben om størrelser", og denne definition var fremherskende frem til 1700-tallet.[12] Men da den matematiske forskning i løbet af 1800-tallet i stigende grad blev præget af logisk strenghed og desuden begyndte at opdyrke nye felter som gruppeteori og projektiv geometri, som ikke primært handler om målelige størrelser, begyndte der blandt matematikere og filosoffer at dukke en række nye definitioner op.[13] I dag arbejder man inden for matematisk filosofi med tre overordnede måder at definere faget på, nemlig en logicistisk, som anser matematik for at høre under logikken, en intuitionistisk, som lægger vægt på de tankerækker og tankebaner, som matematikere følger i deres arbejde med at opnå ny indsigt, samt en formalistisk, hvor det væsentlige er hvordan man håndterer matematiske symboler efter visse grundantagelser. Man er dog langtfra enige om, hvilken af disse overordnede måder giver den bedste forståelse af matematikkens natur.[14]
Ganske mange matematikere er ligeglade med, hvordan matematik skal defineres, eller mener at det er umuligt at gøre.[10] Der er heller ikke enighed om, hvorvidt matematik er videnskab eller kunst.[11] Nogle bruger den simple definition, at "matematik er det som matematikere laver".[10]
Historie
[redigér | rediger kildetekst]
Historisk set er matematikken opstået ud fra behovet for at lave beregninger i handel, for at opmåle land og for at forudsige astronomiske begivenheder. Disse tre behov kan groft relateres til en bred underopdeling[kilde mangler] af matematikken i studiet af algebra, rum og infinitesimalregning.
En vigtig del af grundlaget for den matematiske videnskab blev lagt i antikkens Grækenland, hvor især Euklids lærebog Elementerne fra omkring år 300 f.Kr. skulle vise sig at få kolossal betydning for matematikundervisningen helt frem til engang i 1900-tallet.[16] Bogen er en samling af grundlæggende definitioner, samt udledninger af matematiske objekter og begreber baseret på disse definitioner, udledninger baseret udelukkende på logisk-deduktiv bevisførelse. Herved sikres, at hvis udgangspunktet for en udledning er sand, så bliver resultatet det også. Matematik kom herved til at fremstå som en videnskab som fremlagde absolutte sandheder.[17]
I antikkens Grækenland anså man matematikken for at omhandle og beskrive virkeligheden, og denne forestilling holdt sig til langt op i 1800-tallet. Men nye matematiske opdagelser, bl.a. Cantors arbejde inden for mængdelære med uendelige mængder og Gauss' erkendelse af, at Euklids bevis for det såkaldte parallelpostulat var problematisk, førte til nye måder at anskue matematikken på. Cantors arbejde med uendelige mængder viste sig at medføre en logisk modstrid, som gjorde det nødvendigt at omdefinere aksiom-begrebet, så det fra at udtrykke en absolut sandhed om virkeligheden i stedet blot skulle være fri for modsigelser og ikke længere nødvendigvis beskrive virkeligheden.[18] Gauss' arbejde med geometri førte til udvikling af den ikke-euklidiske geometri, hvor man fx godt kan have flere parallelle linjer gående gennem samme punkt og hvor vinkelsummen i en trekant ikke altid er 180 grader,[19] geometriske egenskaber som senere viste sig anvendelige i Einsteins relativitetsteori.[20]
Udspring, anvendelighed og skønhed
[redigér | rediger kildetekst]
Matematik er i tidens løb udsprunget af en række forskellige praktiske problemer, såsom handel, landmåling, arkitektur og astronomi. I dag kan alle videnskaber fremvise problemstillinger, som kan løses ved hjælp af matematik, og den matematiske videnskab skaber også selv løbende nye sådanne problemstillinger. Det var f.eks. ved at kombinere fysisk forståelse med matematisk logik at fysikeren Richard Feynman indførte brugen af kurveintegraler inden for kvantemekanik. Strengteorien, som forsøger at give en samlet beskrivelse af universets opbygning vha de fire fundamentale naturkræfter, er på lignende vis en stadig inspirationskilde til ny matematisk indsigt.[21]
Noget matematik har kun relevans inden for de områder, hvor den er udviklet, og her kan den bruges til at opnå større indsigt. Men ofte har matematisk indsigt udviklet inden for ét område vist sig anvendelig inden for andre områder. Man skelner her ofte mellem ren matematik og anvendt matematik, men erkendelser inden for den rene matematik viser sig ofte senere at kunne anvendes i praksis, som fx talteori inden for kryptografi.
Den kendsgerning at selv den 'reneste' matematik ofte har praktiske anvendelsesmuligheder har Eugene Wigner kaldt "matematikkens urimelige effektivitet".[22] Som på andre områder har den megen ny videnskabelige indsigt den senere tid ført til en specialisering, så at matematik i dag kan opdeles i flere hundrede underdiscipliner.[23] Inspireret af områder uden for matematikken har mange discipliner inden for anvendt matematik udviklet sig til selvstændige discipliner, såsom sandsynlighedsregning, statistik, operationsanalyse og datalogi.
Euklids bevis for, der er uendeligt mange primtal
- oprindeligt publiceret i hans værk Elementer:[24][25]
Betragt en liste med et vilkårligt, men endeligt antal primtal p1, p2, ..., pn. Hvis P er produktet af alle primtal på listen: P = p1p2...pn, og det antages at q = P + 1, så er q enten et primtal eller ej:
- Hvis q er et primtal, findes der mindst ét primtal, som ikke er på listen.
- Hvis q ikke er et primtal, må der findes en primtalsfaktor p som går op i q. Stod denne faktor p på vores liste, ville den gå op i P (idet P er produktet af alle tal i listen); men p går som sagt også op i P + 1 = q. Hvis p både går op i P og q, så må p også gå op i forskellen mellem de to,[b] som er (P + 1) − P eller 1. Da intet primtal går op i 1, står p ikke på listen. Dermed må der findes yderligere mindst ét primtal.
Hermed er bevist, at der for enhver liste med endeligt mange primtal findes endnu et primtal.
For mange matematisk interesserede er der et aspekt af skønhed knyttet til matematik, og man beskriver faget med udtryk som elegance, æstetik og indre skønhed, foruden enkelhed og almengyldighed. Man finder skønhed i et enkelt og elegant bevis, som fx Euklis bevis for, at der er uendelig mange primtal, eller en snild metode til at øge hastigheden af udregninger, som fx Fast Fourier Transform. Matematikeren G. H. Hardy har udtrykt, at dette aspekt af skønhed i sig selv er nok til at retfærdiggøre studiet af ren matematik, en skønhed der bl.a. kan beskrives med ord som betydning, uforudsethed, uundgåelighed og økonomi.[26]
Matematisk forskning søger ofte at afdække afgørende træk ved et matematisk objekt. Det videnskabelige trofæ man stræber efter er at kunne formulere en sætning, der karakteriserer objektet ud fra disse træk. Eksempler på særligt kortfattede og åbenbarende matematiske bevisførelser er samlet i bogen Proofs from THE BOOK.[27]
Den popularitet, som underholdningsmatematik nyder, er et tegn på, at mange ynder at sysle for sjov med matematiske opgaver. Omvendt støder filosoffer stadig på problemer inden for matematikkens filosofi, fx vedrørende det matematiske bevis' væsen.[28]
Notation, sprog og strenghed
[redigér | rediger kildetekst]
Mange af de symboler og tegn, som bruges i matematisk notation, blev først taget i brug i løbet af 1500-tallet, fx lighedstegnet og større end- og mindre end-tegnene.[c][29] Tidligere var matematisk tænkning blevet skrevet ud i tekst, hvilket faktisk begrænsede mulighederne for nye videnskabelige landvindinger.[30] Det var Euler, som indførte megen af den moderne matematiske notation, en notation som letter den matematiske forståelse for den professionelle. Derimod afskrækkes begyndere inden for faget ofte af notationen, fordi matematisk argumentation både er mere abstrakt og mere kryptisk end sædvanlig sprogbrug,[31] hvor det er nemmere at forstå sammenhængen mellem et ord (fx ko) og den fysiske genstand (her et pattedyr af drøvtyggerfamilien), ordet refererer til. I modsætning hertil er matematiske symboler og begreber abstrakte, uden sidestykker i den fysiske verden,[32] og desuden ofte med udvidede betydninger, hvor et enkelt symbol kan repræsentere flere forskellige handlinger eller begreber.[33]
Eksempel på matematisk fejlslutning
I Holbergs komedie Erasmus Montanus forsøger hovedpersonen, hjemvendt til sin barndoms landsby fra studier i København, at imponere sin mor med denne logiske argumentation:[34]
1. En sten kan ikke flyve
2. Morlille kan ikke flyve
3. Altså er Morlille en sten
Erasmus forsøger at anvende den klassiske modus ponens-logik:
1. p medfører q (hvis Morlille er en sten, så kan Morlille ikke flyve)
2. p er sand (Morlille er en sten)
3. Altså er q sand (altså kan Morlille ikke flyve),
men han får byttet om på punkt 2 og 3. For at berolige sin nu opskræmte mor fortsætter Erasmus:
1. En sten kan ikke tale.
2. Morlille kan tale.
3. Altså er Morlille ingen sten.
Dennegang anvender Erasmus modus tollens-logik:
1. p medfører q (hvis Morlille er en sten, så kan Morlille ikke tale)
2. q er falsk (Morlille kan godt tale)
3. Altså er p falsk (altså er Morlille ingen sten),
med bedre resultat.
Også når man ser bort fra notationen med symboler og tegn kan matematikeres sprog være svært at forstå for begyndere. Almindelige ord som eller og kun har en mere præcis betydning end i dagligsprog, mens andre ord som åben, legeme og gruppe refererer til bestemte matematiske forestillinger, som ikke har med ordenes sædvanlige betydning at gøre. Matematikere bruger også fremmedord som homomorfi og integrabel, som ikke giver mening uden for matematikken. Grunden til, matematikere bruger en særlig notation og et særligt sprog er ønsket om at kunne udtrykke sig med større præcision end hvad dagligsprog tillader. Man taler om matematisk strenghed.[kilde mangler]
Matematisk bevisførelse er dybest set et spørgsmål om logisk strenghed. Bevisførelsen resulterer i sætninger, som er udledt fra aksiomer ved hjælp af systematisk logik. Herved undgår man falske sætninger udledt ud fra fejlslutninger, som der har været mange eksempler på, se tekstboks. Graden af nødvendig strenghed har vekslet gennem matematikkens historie: de gamle grækere forlangte detaljeret bevisførelse, men på Isaac Newtons tid var man begyndt at tage lidt lettere på tingene. Dette medførte efterhånden visse uhensigtsmæssigheder, så at man i 1800-tallet igen vendte sig mod detaljeret logisk analyse og formel bevisførelse. I dag diskuterer matematikere, hvorvidt og hvordan man kan bruge computere til at udlede sætninger: da omfattende og indviklede beregninger er svære at efterprøve, kan beviset for sådanne sætninger være fejlbehæftet, hvis computerens software er fejlbehæftet.[d][35] Der er dog udviklet hjælpeprogrammer (eng: proof assistants), som kan foretage en fuldstændig gennemgang og afprøvning af alle trinene i lange, indviklede beviser, som fx Feit-Thomsons sætning, hvis bevis på tryk fylder mere end 1.000 sider.
Matematiske discipliner
[redigér | rediger kildetekst]I dag er matematik baseret på logik og bevisførelse. Historisk set er matematikken opstået ud fra behovet for at lave beregninger i handel, for at opmåle landområder og jordlodder og for at forudsige astronomiske begivenheder. Disse tre behov kan groft relateres til en bred underopdeling[kilde mangler] af matematikken i studiet af hhv tal, rum og infinitesimalregning, også kaldet algebra, geometri og analyse.[36]
Logik og mængdelære
[redigér | rediger kildetekst]Hvor matematikeres arbejde oprindeligt udelukkende bestod i beregninger, opstod efterhånden et behov for at få formaliseret de regler, man regnede efter. Dette var baggrunden for udviklingen af matematisk logik, hvor filosofiens logiske tænkning anvendes inden for matematiske discipliner. Ud fra nogle få grundlæggende logiske sandheder, kaldet aksiomer, søger man vha logisk argumentation at nå frem til nye sandheder af mere indviklet natur om specifikke matematiske problemstillinger. Omkring år 1900 søgte David Hilbert at formalisere matematikken ved at opstille al matematik i et system af aksiomer, som bl.a. skulle afhjælpe nogle logiske problemer i Euklids geometri, men senere viste Kurt Gödel i sin ufuldstændighedssætning, at dette ikke lader sig gøre. De første årtier af 1900-tallet blev præget af en krise inden for matematikken, hvor man (forgæves, skulle det vise sig) søgte at afdække et sådant fuldstændigt forklarende system, i stil med Hilberts.[37][38]
I mængdelæren beskæftiger man sig med samlinger af objekter. Dette felt blev især udviklet af Georg Cantor i slutningen af 1800-tallet, bl.a. som et forsøg på at opnå en bedre forståelse af uendelighedsbegrebet. Mængdelæren er blevet en vigtig matematisk disciplin, som mange i dag opfatter som et helt afgørende redskab inden for praktisk talt alle områder af matematik.[39]
Kombinatorik
[redigér | rediger kildetekst]
I mange situationer står man over for at skulle udvælge elementer fra en mængde efter visse kriterier, og man kan nu spørge, hvor mange valgmuligheder der er i hver af sådanne situationer. Hvis elementerne skal vælges i en bestemt rækkefølge, som fx de optrædende ved en bestemt festivalkoncert eller farverne i et flags (vandrette eller lodrette) striber, kalder man valgmulighederne for permutationer, og her gælder alment, at hvis man skal udvælge q elementer fra en mængde på n elementer, kan dette gøres på
forskellige måder,[40] hvor størrelsen (læses "n fakultét") er lig produktet af alle tallene fra n til 1:
I andre situationer udvælger man elementer fra en mængde i tilfældig rækkefølge, fx når man fra et almindeligt spil kort deler 13 kort ud til hver af 4 spillere. En sådan hånd af 13 kort kaldes en kombination, og her gælder alment, at hvis man skal udvælge q elementer fra en mængde på n elementer, kan dette gøres på
forskellige måder. I tilfældet med kortspillet er der tale om
eller godt 635 mia forskellige kombinationer.[41]
Sandsynlighedsregning
[redigér | rediger kildetekst]I hverdagen stilles man ofte over for at skulle vurdere, hvor sandsynligt det er at noget bestemt vil indtræffe. Ved mange af sådanne hændelser er det svært eller umuligt at udtale sig præcist om sandsynligheder, fx udfaldet af en fodboldkamp eller et straffespark, mens det i andre situationer godt kan lade sig gøre. Dette gælder fx udfaldet af spil med en terning. De 6 mulige udfald af et terningkast udgør tilsammen udfaldsrummet U for eksperimentet ’at kaste en terning’,
Sandsynlighederne for hvert udfald beskrives af en tilknyttet funktion, kaldet en stokastisk variabel ('stokastisk' hentyder til, at udfaldet af eksperimentet er tilfældigt og altså ikke kan forudsiges). Spiller man med en terning, så er sandsynligheden p for at slå 1 eller 2 eller 3 eller 4 eller 5 eller 6 øjne i hvert tilfælde 1/6, svarende til, at der er tale om et symmetrisk sandsynlighedsfelt. Det gælder her, som for ethvert udfaldsrum, at summen af sandsynlighederne for de forskellige udfald er lig med 1:

Hvis man spiller med to terninger, fås et udfaldsrum med elementer, idet hver terning kan falde på 6 forskellige måder. Normalt vil man ikke i et terningespil, som fx matador eller meyer, skelne mellem udfald med samme øjensum, som fx {1,2} og {2,1}, eller {1,3}, {2,2} og {3,1}, men blot registrere, at summen af øjnene er 3, hhv. 4. Udfaldsrummet for spil med to terninger kan derfor opdeles i 11 delmængder, kaldet hændelser, se figur.[42]
Det simpleste eksperiment inden for sandsynlighedsregning er kast med en mønt, som har to mulige udfald, plat eller krone, og i tilfælde af en symmetrisk mønt hver med sandsynligheden s=½. Hvis man udfører et eksperiment med at kaste en mønt 5 gange, får man således et udfaldsrum med forskellige udfald. Disse fordeler sig på hændelserne '5 krone', '4 krone', '3 krone' osv., og sandsynlighederne for disse hændelser kan beskrives vha binomialfordelingen[43]
hvor q er antal krone, n er antal kast, mens s er sandsynligheden for krone i et kast.
Aritmetik og talteori
[redigér | rediger kildetekst]Opgave i aritmetik
Udregn denne brøk:
Rækkefølge for udregninger:[44]
1. parenteser
2. potenser og rødder
3. multiplikation og division
4. addition og subtraktion
Brøken kan omskrive således:
Først udregnes potenser og rødder,
dernæst indre parentes, ved subtraktion,
dernæst ydre parentes, først multipliceres,
dernæst adderes
og til slut divideres


Mennesker og samfund har fra de tidligste tider haft brug for at kunne håndtere tal. Først indførtes de naturlige tal 1, 2, 3, 4 osv.[45] Senere blev tallet 0 indført,[46] og negative tal,[47] foruden rationale tal som 1/2 og -2/3, samt de reelle tal[48] som fx og pi, og senest de komplekse tal,[49] som udvider talbegrebet fra at omfatte punkter langs en en-dimensionel tallinje til at omfatte punkter i en to-dimensionel plan.[47] Med alle disse grupper af tal kan man lave beregninger ved hjælp af de fire regningsarter addition, subtraktion, multiplikation og division (også kaldet hhv at lægge sammen, trække fra, gange og dividere). Ud over regningsarterne kan man foretage procentregning, uddragning af rødder og potensopløftning.
Ved beregninger er det især divisionsoperationen, der kan være tidkrævende, og matematikere begyndte tidligt at undersøge mængden af divisorer for heltal, altså hvilke heltal der går op i andre heltal. Dette førte til studiet af primtal (heltal uden divisorer), som er en klassisk disciplin inden for talteori, men fx også studiet af fuldkomne tal (heltal, hvor summen af divisorerne er lig tallet, se figur).[kilde mangler]
De gamle ægyptere havde udviklet et system til brøkregning baseret på stambrøker (brøker med tælleren 1), og multiplikationer blev udført efter et system af fordoblinger og additioner ved hjælp af tabeller af formen 2/n; man brugte fx brøken 256/81 som tilnærmelse til pi.[50]
De gamle grækere opdagede,[51] at ikke kan skrives som en brøk, at det altså ikke er et rationalt tal, men et irrationalt, og deres opdagelse af, der findes irrationale tal menes på den tid at have afskedkommet en forskningsmæssig krise inden for matematik.[52]
Algebra
[redigér | rediger kildetekst]Algebra er en vigtig matematisk disciplin, som mange skoleelever i en eller anden form stifter bekendtskab med, i Danmark typisk i løbet af gymnasiet, i USA i high school. Undervisningen i algebra bygger videre på elevernes kendskab til aritmetik, men hvor aritmetik drejer sig om at behandle bestemte tal,[53] arbejder man i algebra med tal med ukendt, konstant eller skiftende størrelse.[54] Ved hjælp af disse algebraiske størrelser, samt en særlig algebraisk notation og de aritmetiske regneregler, er det muligt at beskrive forholdet mellem forskellige talstørrelser på formel og præcis måde, og dermed angive almene løsninger for en lang række beregningsopgaver. Inden for såvel naturvidenskab i almindelighed som matematik i særdeleshed findes der mange kvantitative sammenhænge, såsom andengradsligningen (se figur), som er beskrevet ved hjælp af algebraiske ligninger. Undersøgelsen af metoder til at løse ligninger fører til studiet af abstrakt algebra. Det for fysikerne vigtige begreb vektorer, der er generaliseret til vektorrummet og studeret i lineær algebra, tilhører de to grene algebra og rum.
Elementær algebra
[redigér | rediger kildetekst]
2. Koefficient
3. Led
4. Operator
5. Konstant
x, y: Variable.
Opgave i algebra
Spørgsmål: Hvis B er fire år ældre end A, og de tilsammen er tolv år, hvor gamle er så A og B?
Svaret findes ved at opstille to ligninger med to ubekendte, nemlig A’s alder x og B’s alder y:
Ligning 1
Ligning 2
Ligning 2 kan omskrives til:
Nu kan højre side af de to ligninger sættes lig hinanden:
som kan omskrives til:
eller:
og ved indsættelse i Ligning 1:
De tre forskellige gangetegn betyder det samme:
De fire forskellige divisionstegn betyder det samme:
- og man kan ikke dividere med 0.[55]
Inden for algebra anvendes en særlig notation og sprogbrug til behandling og udregning af talstørrelser, se figuren med udtrykket . Udtrykket er opbygget af tre led, som hver er adskilt af operatorerne + eller –, og hvert led består af et antal faktorer, som kan være enten koefficienter, variable eller eksponenter. Faktorerne skal ganges med hinanden, men gangetegnene udelades normalt og er underforståede, når der ikke er mellemrum mellem faktorerne. Med leddet menes underforstået , mens der med menes .[56][57] En koefficient er en konstant (her kendt) talværdi, som skal ganges med den eller de variable, som har ukendte talværdier, og som eventuelt skal opløftes til den (her kendte) potens, som eksponenten angiver.[58]
I algebra bruges bogstaver til alle slags faktorer. De første bogstaver i alfabetet (fx , og ) bruges typisk til koefficienter eller konstanter, mens dem sidst i alfabetet (fx , og ) bruges til variable,[59] ofte skrevet i kursiv.[60]
Beregning fungerer inden for algebra på samme måde som inden for aritmetik,[61] dvs addition, subtraktion, multiplikation, division og potensopløftning.[62]
Led med variable med højest potens skrives til venstre, fx til venstre for . Koefficienter lig med 1 udelades normalt (fx skrives som ),[63] ligesom eksponenter lig med 1 (fx skrives som ).[64] Er eksponenten nul, er resultatet altid 1 (fx er altid lig med 1),[65] dog undtaget , som ikke giver mening.
Elementær algebra er en udbygning af aritmetik,[66] som kan håndtere beregninger af mere overordnet karakter, idet bestemte tal erstattes med mere generelle bogstaver, jf disse eksempler med variable:
- Variable kan symbolisere tal med ukendt værdi. Hvis fx temperaturen D en dag er 10 grader højere end temperaturen F den foregående dag, kan sammenhængen mellem temperaturerne beskrives som .[67]
- Variable gør det muligt at beskrive et problem generelt,[68] uden at angive størrelsen af de tal som indgår. Man kan fx angive 5 minutter som sekunder. Et mere generelt algebraisk udtryk for antallet af sekunder er , hvor m er antal minutter.
- Variable gør det muligt at beskrive matematiske sammenhænge mellem størrelser som varierer.[69] Fx er sammenhængen mellem en cirkels omkreds c og diameter d givet ved udtrykket .
- Variable kan bruges til at beskrive matematiske egenskaber. Fx er det en grundlæggende egenskab ved addition, at den er kommutativ, således at addendernes orden er ligegyldig, hvilket vha algebra kan skrives .[70]
Komplekse tal
[redigér | rediger kildetekst]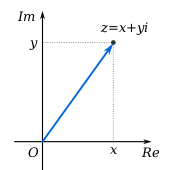
I 1500-tallet forsøgte italienske matematikere at finde rødder til tredje- og fjerdegradsligninger og stødte på det problem, at løsningerne i visse tilfælde indebar kvadratrødder af negative tal, hvilket er meningsløst.[71][72]Man søgte bl.a. efter en metode til at finde rødder i tredjegradsligninger af formen
En sådan blev fundet, af både Scipione del Ferro omkring 1515, Niccolò Tartaglia i 1539 [71] og af Gerolamo Cardano i 1545:[73]
Så længe udtrykket er positivt, er der ikke problemer, men er det negativt, kan man ikke tage kvadratroden af det. Italieneren Rafael Bombelli fik dog den mærkelige ide at regne videre, selv når udtrykket under kvadratroden var negativt. Han kiggede på ligningen
som vha Cardanos formel kunne omskrives til
Bombelli fandt nu en sammenhæng mellem udtrykkene og , idet[74]
,
samt tilsvarende
og kunne nu indsætte i udtrykket ovenfor
- ,
som er løsning til ligningen. Så på trods af, udregningerne indeholder meningsløse kvadratrødder af negative tal, kommer der et brugbart resultat ud af dem. Dette førte til, man indførte en såkaldt imaginær enhed
og ved hjælp af den en helt ny slags tal, de komplekse tal , der skrives på formen
Den franske filosof René Descartes tog afstand fra kvadratrødder af negative tal og indførte betegnelsen "imaginær" for dem i afhandlingen La Géométrie fra 1637.[75][76] Det er dog hans betegnelse "imaginær" der i dag ligger til grund for valget af bogstav til tallet i.
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
Hvor de reelle tal , og deres delmængder, de naturlige tal , de hele tal og de rationale tal alle kan opfattes som punkter på en tallinje, skal de komplekse tal opfattes som punkter i en todimensionel talplan,[77] se figur. Med komplekse tal kan man udføre samme slags operationer som med reelle tal, dvs med de fire regningsarter. Addition af komplekse tal svarer fx til parallelforskydning i planet, mens multiplikation svarer til en drejning efterfulgt af en strækning omkring nulpunktet.[78] I modsætning til polynomier af reelle tal, som ikke nødvendigvis har rødder, har komplekse polynomier altid rødder, og således har et n-te gradspolynomium altid n rødder.[79]
Det komplekse talbegreb blev i midten af 1800-tallet af den irske matematiker W.R. Hamilton udviklet til kvaternion-begrebet, hvor et tal kan opfattes som et punkt i et fire-dimensionelt rum:
hvor a, b, c og d er reelle tal, mens i, j og k er kvaternion-enheder, se tabel.
Vektorer
[redigér | rediger kildetekst]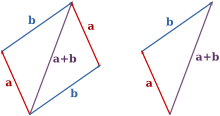

Det er ofte hensigtsmæssigt at kunne regne med størrelser, som både angiver en størrelse og en retning, fx når meteorologer laver kort over vindforhold eller når en flyveleder skal holde styr på flyene omkring en lufthavn.[80] Hertil anvender man vektorer, som gerne afbildes som pile, med en retning og længde. I matematisk notation bruges enten en pil over bogstavet eller fed skrift:
Regning med vektorer bruges mange steder inden for især fysik og grafik, og vektorbegrebet blev udviklet i første halvdel af 1800-tallet, i et samarbejde mellem matematikere og fysikere.[81]
Man kan regne med vektorer på nogenlunde samme måde som med tal, idet man kan lægge vektorer sammen, trække dem fra hinanden og gange dem med hinanden. Addition af to vektorer kan udføres geometrisk ved at tegne vektorerne op, så de ligger i forlængelse af hinanden, og summen bliver så den vektor, som er defineret af det tilsvarende parallelogram, se figur. Ganges en vektor a med et tal (også kaldet en skalar) k, fås en vektor ka, som er parallel med a, har længden k|a| og hvis retning i forhold til a er bestemt af, om k er positiv eller negativ. Skal man trække en vektor b fra en vektor a, begynder man med at gange b med -1, og så lægge de to vektorer sammen: a - b = a + (-b)[82]
Ofte vil man afbilde vektorer i et koordinatsystem, og nu kan vektorberegninger udføres med koordinater, enten vist som en søjle (kolonne):
eller en række af vektorkoordinater: eller . Tredimensionelle vektorer repræsenteres på lignende vis:
Man kan også arbejde med vektorer i højere dimensioner, her en almen repræsentation af n-dimensionel vektor:
Abstrakt algebra
[redigér | rediger kildetekst]Som det er fremgået, er talbegrebet flere gange gennem matematikkens historie blevet udvidet: først brugte man kun hele tal, dernæst udvidede man med brøker til rationale tal, dernæst med irrationale tal til reelle tal, dernæst med kvadratrødder af negative tal til komplekse tal. Siden er også de firedimensionelle kvaternioner kommet til, for ikke at nævne de ottedimensionelle oktonioner. Det har faktisk vist sig principielt umuligt at konstruere et talbegreb som er tilpas omfattende til at beskrive alle tænkelige matematisk problemstillinger, og det er i det lys, den abstrakte algebra har udviklet sig.[83]
I abstrakt algebra beskæftiger man sig overordnet med mængder og regneregler (kompositioner), fx en binær operation •, der ud fra to elementer m og n fra en given mængde konstruerer et nyt element m • n, som gerne må tilhøre samme mængde, men ikke nødvendigvis gør det. En sådan operation vil være underlagt regler analoge til dem, som gælder for sædvanlig addition eller multiplikation, mens naturen af det der kommer ud af operationen ikke nødvendigvis er kendt, især hvis de to elementer m og n ikke er af enkel natur.[83]
Eksempel på matematisk struktur
En gruppe er en mængde, fx de hele tal, som er udstyret med en regneregel og som for vilkårlige elementer a, b og c opfylder disse tre aksiomer:
1. Regnereglen er associativ, dvs
2. Der findes et neutralt element e, således at
3. Der findes et inverst element a', således at
Hvis vi kombinerer mængden af hele tal og regnereglen addition, får vi en gruppe (Z,+):
1.
2. (e er tallet 0)
3. (a' har modsat fortegn af a)
Får vi også en gruppe (Z, ), hvis vi kombinerer mængden af hele tal med regnereglen multiplikation?
1.
2. (e er tallet 1)
3. (a' er den reciprokke af a)
Nej, i regel 3 går det galt: den reciprokke værdi af et heltal er kun et heltal for tallet 1, så (Z, ) er ikke en gruppe.[84]
Hvis man spiller matador med to terninger, står på plads k og fx slår m og n øjne, kan man enten først flytte m pladser og dernæst n pladser, eller omvendt, eller man kan flytte alle øjnene på en gang, igen på to måder, så der i alt er fire måder at nå sin nye plads på. Hvis man med betegner den operation at flytte sin bil et antal pladser, bliver den nye plads nemlig enten[83]
- eller , dvs den associative lov er opfyldt, eller
- eller , dvs den kommutative lov er opfyldt.
Algebra kan ofte knyttes til geometri, og undertiden også til fysiske objekter fra den virkelige verden. Fra geometrien kendes de fem regulære polyedre: tetraeder, hexaeder, oktaeder, dodekaeder og ikosaeder. Inden for krystallografi kan disse polyedre vha forskellige symmetrier underopdeles i 219 krystallografiske grupper, hvilket er et antal man også er nået frem til inden for abstrakt algebra. Dette er bemærkelsesværdigt i lyset af, at algebra ikke på nogen måde forholder sig til eller lader sig begrænse af den fysiske virkelighed. Lignende eksempler kan findes i kemi, atomfysik og kvantemekanik.[83] I abstrakt algebra arbejder man med overordnede strukturer, for eksempel:
- en gruppe er en mængde med én tilknyttet binær operation, fx , mængden af hele tal og operationen addition, se tekstbox,
- en ring er en mængde med to tilknyttede binære operationer, fx , mængden af rationale tal og operationerne multiplikation og addition,
- et legeme er en mængde, hvorpå alle fire regnearter kan udføres.[85]
De rationale tal, de reelle tal og de komplekse tal er alle eksempler på legemer.
 |
 |
 |
 |
||
| Kombinatorik | Abstrakt algebra | Gruppeteori | Grafteori | Ordningsteori | Algebra |
Geometri
[redigér | rediger kildetekst]
Sammen med aritmetik er geometri en af matematikkens ældste discipliner. Geometri betyder landmåling, og netop nøjagtig landmåling var af stor vigtighed i de tidlige agerbrugsbaserede flodkulturer i Egypten og Mesopotamien: "Hvordan opdeler man en mark i lige store stykker? Hvordan prissætter man et stykke jord ud fra dets areal? Hvilken af disse to grunde ligger nærmest floden? Hvordan skal den kommende kanal planlægges, så den bliver så kort som muligt?"[86] I geometri undersøger man plane eller rumlige figurer mht størrelser, form, afstand og indbyrdes placering.[87]
Studiet af rummet starter med studiet af geometri, først den euklidiske geometri og trigonometri i det sædvanlige tredimensionale rum, men senere også generaliseret til ikke-euklidisk geometri som spiller en central rolle i den generelle relativitetsteori. De moderne områder differentialgeometri og algebraisk geometri generaliserer geometri i forskellige retninger: differentialgeometri fremhæver begreberne koordinatsystemer, glathed og retning, mens geometriske objekter i algebraisk geometri beskrives som løsninger til et sæt af ligninger. Gruppeteori undersøger på en abstrakt måde begrebet symmetri og giver en sammenhæng mellem studiet af rum og struktur. Topologi giver en sammenhæng mellem studiet af rum og studiet af ændring ved at fokusere på begrebet kontinuitet.[kilde mangler]
Syntetisk og analytisk geometri
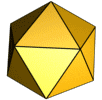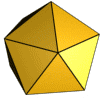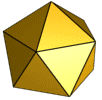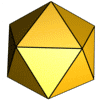
[redigér | rediger kildetekst]Det var i oldtidens Grækenland, geometrien blev udviklet til perfektion, som beskrevet i Euklids Elementer fra omkring 300 f.Kr. Helt frem til et stykke op i 1800-tallet var geometri stadig euklidisk og beskæftigede sig med punkter, linjer, cirkler, planer, afstande, vinkler, flader og kurver som grundlæggende begreber.[88] Den græske matematiker Theaitetos studerede regulære polyedre, dvs. rumlige legemer sammensat af regulære og kongruente polygoner, og han opdagede, at der kun findes fem regulære polyedre, de såkaldte platoniske legemer. Platon har lagt navn til legemerne, fordi han senere postulerede, de fire af legemerne symboliserede de fire elementer, man dengang mente alt stof var sammensat af.[89]
- De fem platoniske legemer:
-
Tetraeder: 4 trekanter
-
Heksaeder: 6 kvadrater
-
Oktaeder: 8 trekanter
-
Dodekaeder: 12 femkanter
-
Ikosaeder: 20 trekanter

Hvor algebra og geometri i lange perioder af matematikkens historie ikke havde særligt meget med hinanden at gøre, sker der i løbet af 1600-tallet noget afgørende. Franskmanden Descartes udgav i 1637 en lærebog i geometri,[49] hvor han indførte koordinatsystemet og definerede planen med en x-akse henad og en y-akse opad. Hvor geometri tidligere udelukkende blev udført vha passer og lineal og i overensstemmelse med de euklidiske aksiomer, såkaldt klassisk eller syntetisk geometri, kunne de to områder nu knyttes tæt sammen, idet geometriske figurer kunne beskrives vha. algebraiske ligninger og kartesiske koordinater, de sidste opkaldt efter Descartes, se figur, og denne nye geometri kaldes analytisk geometri.[90]
Både geometrisk og algebraisk set er det nemt at gå fra at betragte et todimensionelt til et tredimensionelt koordinatsystem, svarende til man går fra at betragte plane til at betragte rumlige figurer. Geometrisk set er det derimod ikke nær så ligetil at gå videre, og betragte firedimensionelle legemer, mens dette uden videre lader sig gøre inden for algebra. Denne mulighed blev benyttet i Einsteins relativitetsteori, hvor den fjerde dimension er tiden.[91]
Ikke-euklidisk geometri
[redigér | rediger kildetekst]
Euklids geometri var baseret på et antal selvindlysende sandheder, eller aksiomer, som fx at "et linjestykke kan konstrueres ved at forbinde to vilkårlige punkter", eller "et linjestykke kan forlænges i det uendelige til begge sider". Men et af Euklids aksiomer voldte gennem lang tid matematikerne problemer, nemlig det såkaldte parallelpostulat: "Igennem et givet punkt kan man tegne én og kun én linje, som er parallel med et givet linjestykke."[92] Dette postulat var ikke så selvindlysende som Euklids øvrige aksiomer, og mange forsøgte at opstille et bevis for postulatet, først arabiske matematikere i 11. århundrede og senere europæiske matematikere gennem middelalderen og renæssancen.[93] Først omkring 1815 påviste Gauss og Schweikart, uafhængigt af hinanden, at Euklids aksiom simpelthen ikke var korrekt, og fremlagde grundlaget for det, som Gauss kaldte ikke-euklidisk geometri.[94]
Denne nye geometri kunne deles i to, nemlig elliptisk geometri, hvor man undersøger figurer på en kugleflade, og hvor vinkelsummen i en trekant viser sig at være større end 180 grader, dels hyperbolsk geometri, hvor man undersøger figurer på konkave flader, fx en sadel, og hvor vinkelsummen i en trekant viser sig at være mindre end 180 grader.[95]
Fraktaler
[redigér | rediger kildetekst]
I begyndelsen af 1900-tallet opdagede man overraskende egenskaber ved simple geometriske figurer, hvis disse figurer blev ændret vha gentagne iterationer. Dette gælder fx Kochs snefnug, hvor hver af siderne i en ligesidet trekant i hver iteration dele i tre, hvor så det midterste stykke fjernes og erstattes af en ny mindre ligesidet trekant, se figur. Det viser sig, at i takt med man laver flere og flere iterationer går den fremkomne figurs areal mod 8/5 af den oprindelige trekants areal, mens omkredsen går mod uendelig. Her har man altså at gøre med en figur med endeligt areal, men uendelig stor omkreds.[96]

Den franske matematiker Gaston Julia studerede i 1920-erne iterationer af komplekse andengradspolynomier af typen
og opdagede, at størrelsen af c er afgørende for, om de fremkomne talrækker
går mod uendelige eller endelige værdier. Efter ham er Juliamængden opkaldt, som er grænsen mellem talrækker der ved iteration går mod uendelig (divergerer) og talrækker der ikke går mod uendelig (konvergerer),[97] se eksempel i figur. Julia og hans samtidige kollega P. Fatou var hæmmet af, det store regnearbejde ved disse studier skulle udføres i hånden, så da Benoit Mandelbrot 60 år senere genopdagede Fatous og Julias arbejde, i forbindelse med analyse af kaotisk støj inden for telekommunikation, kunne han bruge computerkraft til at videreføre deres tanker, med det som Mandelbrot nu kaldte fraktaler. [98] Mandelbrotmængden er en afbildning i den komplekse talplan af de værdier af c, opdelt i komponenterne
som adskiller konvergerende fra divergerende værdier. Mandelbrot benyttede i sine afbildninger oprindeligt kun farverne sort (for konvergerende c-værdier) og hvid (for divergerende c-værdier), men i 1980-erne fandt amerikaneren J.H. Hubbard på at farvelægge Mandelbrots hvide punkter efter, hvor mange iterationer der skulle til før talrækken divergerede, hvilket har afstedkommet de ofte meget smukke afbildninger af fraktaler.[99]

En grundlæggende egenskab ved fraktaler er deres selv-similaritet, det at deres former hele tiden gentages i mindre og mindre skala. Dette fænomen ses også mange steder i naturen, fx i floders erosionsmønstre eller et lyns bane gennem luften, foruden i udformningen af mange planter, fx bregneblade og blomkålens frugt. Mandelbrot stillede allerede i 1960-erne i en artikel spørgsmålet: Hvor lang er Storbritanniens kystlinje? Svaret afhænger selvfølgelig af, hvilket landkort man bruger til at måle kystlinjen ud fra, sådan at jo mere detaljeret kortet er, jo længere bliver kystlinjen, på samme måde som omkredsen af Kochs snefnug øges for hver ny iteration.[100]
 |
 |
 |
 |

|
| Geometri | Trigonometri | Differentialgeometri | Topologi | Fraktalgeometri |
Analyse og infinitesimalregning
[redigér | rediger kildetekst]


I begyndelsen af 1700-tallet påstod astronomen Edmund Halley, på baggrund dels af den komet han selv så i 1682, dels af historiske optegnelser af kometpassager i 1531 og 1607, at der i alle tilfælde var tale om den samme komet, at den havde en omløbstid omkring solen på 76 år, og at den derfor ville vise sig igen i 1758.[101] Dette fik andre astronomer til at lave deres egne beregninger på, hvornår kometen ville vise sig, og et af problemerne var her at beregne placeringen af et himmellegeme som bevæger sig i en elliptisk bane og derfor aldrig bevæger sig med konstant hastighed, men enten hvert øjeblik øger sin hastighed, på vej ind mod solen, eller hvert øjeblik taber i hastighed, på vej væk fra solen, se figur.[102] Det skulle vise sig, at sådanne matematiske problemer med størrelser, som hele tiden ændrer sig, kunne løses, hvis man inddelte planetens bane i små intervaller, og lod størrelsen af intervallerne gå mod 0, såkaldte infinitesimaler. Så i infinitesimalregning regner man i princippet med uendeligt små størrelser - og dette har vist sig at have praktisk anvendelse inden for en lang række fagområder, ikke kun fysik og astronomi, men fx også økonomi.[103]
Funktionsanalyse
[redigér | rediger kildetekst]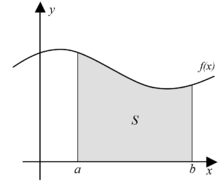
Ved problemer som det ovennævnte er det nødvendigt at kende sammenhørende værdier for et (himmel-)legemes position eller hastighed til bestemte tidspunkter. Det var bl.a. med dette formål, man indførte begrebet matematisk funktion. Her knyttes to talmængder, definitionsmængden og værdimængden, sammen ved hjælp af en regneforskrift, som fører fra et element i definitionsmængden til et element i værdimængden;[104] sagt med andre ord er definitionsmængden input og værdimængden output for regneforskriften. Man afbilder ofte funktionen som en graf, se figur.
Analyse af funktioner er en vigtig disciplin, som også indgår i gymnasieelevers matematikundervisning. Man vil typisk analysere en funktion ved at kigge på dens graf, og undersøge[105]
- hvad der er definitionsmængde og værdimængde for funktionen,
- hvor funktionen skærer koordinatsystemets akser,
- i hvilke intervaller funktionen er monoton, dvs. voksende eller aftagende, og om der er ekstremumspunkter (maksimale eller minimale værdier),
- om funktionen nærmer sig asymptotisk til akser eller linjer,
- om funktionen er symmetrisk, enten omkring en linje eller et punkt.
Blandt de simpleste funktioner er lineære funktioner af typen
som fx kan bruges til at beskrive dagligdags situationer som hvor meget man gennem en bestemt periode skal betale i husleje eller p-afgift, idet så er tiden, er beløb pr måned eller minut, og et evt depositium eller startgebyr. Lineære funktioner bruges ofte til at beskrive en sammenhæng mellem to variable, fx ud fra daglige målinger af udendørs temperatur og forbrug af fjernvarme eller ispinde.
Blandt de meget anvendte funktioner er polynomierne, som generelt kan skrives
hvor er konstanter, og osv er heltal, mens er den variable.[106] Nøjes man med de to sidste led i ovenstående, fås en lineær funktion, som altså kan betragtes som et såkaldt førstegradspolynomium. Tager man de tre sidste led, fås et andengradspolynomium.
Differentialregning
[redigér | rediger kildetekst]
Opgave i differentialregning
En mobiltelefon tabes fra et vindue i et højhus. Hvor længe varer det, før mobilen rammer jorden 20 m længere nede? Og med hvilken hastighed sker det?
Galileis faldlov udtrykker højden som funktion af tiden , idet er starthøjden, og er tyngdeaccelerationen:[107]
Ved at omarrangere ligningen er tiden altså givet ved:
Indsættes m og m/s2, fås
så mobilen falder til jorden på 2,02 sekunder. Hastigheden fås ved at differentiere faldloven:
så mobilen rammer jorden med hastigheden -19,8 m/s.
Vil man fortsætte med at analysere en funktion, kan man undersøge grafens hældning i et bestemt punkt , dvs hældningen af en tangent, som rører grafen, se figur. Denne hældning angiver, hvorledes funktionen ændrer sig omkring punktet, og den kan beskrives med dette udtryk, hvor det græske bogstav bruges til at angive en (lille) ændring i funktionsværdien (y-værdien), , når man på x-aksen går det lille skridt fra til ():[108]
Denne brøk kaldes for differenskvotienten for omkring . Hvis funktionen , og dermed også dens graf, er sammenhængende og ikke knækker i , vil differenskvotienten have en grænseværdi, når går mod , kaldet differentialkvotienten for i :[109]
Når en sådan grænseværdi findes, siger man at funktionen er differentiabel i , og funktionen kaldes den afledede funktion til . Størrelsen er et i princippet uendeligt lille tal, en såkaldt infinitesimal. Et problem ved differentialregning er netop, at nævneren i differenskvotienten går mod 0, når man skal udregne grænseværdien, og man kan jo ikke dividere med 0. For mange funktioners vedkommende er det dog muligt at omskrive differenskvotienten, så leddet forsvinder fra nævneren, fx for funktionen :
Når går mod , går differenskvotienten for således mod .[110]
Eksempler på hyppigt brugte afledede funktioner er:[111]
Man kan anvende de algebraiske regnearter på funktioner på samme måde som på tal, og differentialkvotienterne kan udregnes efter følgende regler:[112]
- (konstant gange funktion)
- (sum af to funktioner)
- (forskel mellem to funktioner)
- (produkt af to funktioner)
- (kvotient mellem to funktioner)
- (sammensat funktion - kædereglen)[113][114]
Regning med differentialkvotienter finder udstrakt anvendelse inden for fysik, men bruges også inden for mange andre praktiske områder, fx optimering i forbindelse med arealudnyttelse eller materialeforbrug, eller inden for økonomi og psykologi.[115]
Integralregning
[redigér | rediger kildetekst]En meget anvendt type funktionsanalyse er at bestemme arealet under funktionens graf. I den højre figur under afsnit Funktionsanalyse herover, med en bils hastighed som funktion af tiden, vil arealet S svare til den tilbagelagte vejstrækning i tidsrummet a til b. Kurven kunne også repræsentere forbrug af fx vand, el eller varme pr tidsenhed, og arealet S ville så svare til det samlede forbrug i tidsrummet a til b.
På figuren herover er en sådan funktions areal under grafen tilnærmet med søjler med ens bredde , dels med funktionsværdier over grafen, som lagt sammen giver en såkaldt oversum , dels med funktionsværdier under grafen, som tilsvarende sammenlagt giver en såkaldt undersum . I animationen gøres søjlerne efterhånden smallere og mere talrige, og man kan vise, at hvis funktionens graf er sammenhængende, eller kontinuert, i intervallet fra a til b, så vil oversummer og undersummer efterhånden mødes i en grænseværdi kaldet integralet af funktionen over intervallet fra a til b:[117]

Hvor summationstegnet symboliserer en sum af et endeligt antal elementer, symboliserer integraltegnet (også kaldet et langt s) således en sum af uendeligt mange elementer. Funktioner med denne egenskab kaldes integrable funktioner, og når man på denne måde integrerer en funktion , vil man ofte kunne gøre det vha. en såkaldt stamfunktion , idet integralet så er lig stamfunktionens tilvækst på intervallet a til b (se figur):[118]
Integrable funktioner hænger nøje sammen med differentiable funktioner, idet det at integrere en funktion er det modsatte af at differentiere den, hvilket er udtrykt i infinitesimalregningens hovedsætning. Når man differentierer en funktion , fås differentialkvotienten , og når man integrerer denne funktion , fås igen stamfunktionen . Ligesom i differentialregning gælder i integralregning visse regneregler for stamfunktioner:[119]
Integralerne i de tre linjer herover indeholder ikke grænser, fx a og b, og er såkaldt ubestemte integraler, i modsætning til integralerne i de to foregående linjer, som indeholder grænser og derfor er såkaldt bestemte integraler. Bestemte integraler er altså tal, nemlig arealer under funktionskurver, fx i et interval fra a til b, mens ubestemte integraler blot er regneforskrifter – som så kan bruges til udregning af sådanne arealer.[120]
Mens det i differentialregning altid er muligt at opskrive et funktionsudtryk for en funktions diffentialkvotient, gælder dette i integralregning kun for visse funktioner, omend mange. Skal man integrere et produkt af to funktioner, kan det gøres således:[121]
Og kædereglen for differentiation af sammensatte funktioner kan også bruges, hvis man skal finde frem til en stamfunktion, ved substitution:[122]
Eksempler på hyppigt brugte stamfunktioner er:
Generelt gælder for brøker med en funktion i nævneren og dens afledede i tælleren:
Differentialligninger
[redigér | rediger kildetekst]Mange praktiske situationer kan beskrives kvantitativt vha en funktion og dens afledede funktion. Fx vil en kande med varm te jo efterhånden stå og blive afkølet. Fra fysikkens varmelære vides, at afkølingens hastighed har at gøre med forskellen på teens temperatur og den omgivende lufts temperatur. Dette kan skrives[123]
hvor er teens temperatur som funktion af tiden , er teens afkølingshastighed, fx målt i grader pr minut, er lufttemperaturen og en proportionalitetskonstant, som bl.a. afhænger af luftens, tepottens og teens varmeledningsevne og varmefylde. I ligningen indgår altså både funktionen og dens afledede , og en sådan ligning kaldes en differentialligning.
En hyppigt forekommende type af differentialligning er
som for fx kan beskrive, hvordan størrelsen af en kapital indsat til bestemt rente vokser med tiden. Er , kan ligningen fx beskrive henfald af stråling fra et radioaktivt materiale. Man kan vise, at løsninger til ligningen er funktioner af typen[124]
hvor er en konstant og er eksponentialfunktionen.
Skal man beskrive væksten af en population, af fx mennesker eller dyr, vil populationen jo vokse med en hastighed, der har at gøre med populationens størrelse, fx
som giver eksponentiel vækst. Dette kan fint beskrive radioaktivt henfald, hvor antal radioaktive partikler går mod 0, eller forrentning af en kapital, hvor kapitalens størrelse med tiden går mod uendelig. Men i mange situationer vil der være grænser for væksten, fx som følge af, der kun er så og så meget plads eller mad til rådighed. Her må tallet i udtrykket ovenfor aftage, efterhånden som populationen vokser, fx lineært som , hvor har at gøre med vækstraten og (for maksimum) står for den øvre grænse for væksten. Differentialligningen kan så i stedet skrives
og man kan vise, at denne ligning har løsningen
Denne ikke-eksponentielle form for vækst kaldes logistisk vækst.[125]
I differentialligninger af typen
kan det svare sig at omskrive vha den symbolske brøk for differentialkvotient
Selvom udtrykket t.v. for lighedstegnet ikke er nogen egentlig brøk, har det vist sig, man godt kan regne med den som sådan, og omskrive ovenstående til
Denne metode kaldes separation af de variable.[126]
Computernes indflydelse
[redigér | rediger kildetekst]For at tydeliggøre og undersøge matematikkens fundament udviklede man områderne mængdeteori, matematisk logik og modelteori.
Da computere i sin tid blev opfundet, blev flere omkringliggende problemer tacklet af matematikere, og det ledte til områderne beregnelighed og informationsteori. Mange af disse spørgsmål er nu undersøgt under teoretisk datalogi.
Foruden ved numerisk analyse har computere også hjulpet til ved emner som kaosteori, som handler om at mange dynamiske systemer i naturen adlyder love, der gør, at deres adfærd bliver uforudsigelig i praksis, selvom det er deterministisk i teorien. Kaosteori er tæt forbundet med fraktal geometri.
Se også
[redigér | rediger kildetekst]Nedenstående gruppering af emner repræsenterer én måde[bør uddybes][kilde mangler] at organisere matematikkens grene på.
Tal
[redigér | rediger kildetekst]- Tal – Naturlige tal – Heltal – Rationale tal – Reelle tal – Komplekse tal – Legemer – Kvaternioner – Oktonioner – Sedenioner – Hyperreelle tal – Surreelle tal – Ordinaltal – Kardinaltal – Heltalsfølge – Matematiske konstanter – Talnavne – Uendelig
Struktur
[redigér | rediger kildetekst]Diskret matematik
[redigér | rediger kildetekst]- Kombinatorik – Mængdeteori – Sandsynlighedsregning – Statistik – Beregnelighed – Diskret matematik – Kryptologi – Grafteori – Spilteori
Diverse
[redigér | rediger kildetekst]
- Matematisk sætning
- Andengradsligning
- Tredjegradsligning
- Matematiker
- Matematisk skønhed
- Matematikkens historie
- Matematisk notation
- Königsbergs syv broer
Litteratur
[redigér | rediger kildetekst]Når et skolebarn har lært at lægge naturlige tal sammen, dvs at addere dem, er det i stand til at forstå og ved afprøvning besvare spørgsmålet: ”Hvilket tal skal man lægge til 3 for at få 5?” Systematisk besvarelse af sådanne opgaver kræver dog, man indfører et nyt begreb: det at trække fra, eller subtraktion. Nu kan spørgsmålet stilles på denne måde: ”Hvad er 5 minus 3?” Straks man har defineret denne subtraktion, kan man også stille spørgsmålet: ”Hvad er 3 minus 5?” Nu føres man mod negative tal, og dermed ud over den grundlæggende regning.
Udenlandsk
[redigér | rediger kildetekst]- Davis, Philip J.; Hersh, Reuben: The Mathematical Experience. Birkhäuser, Boston, Mass., 1980. En skånsom introduktion til matematikkens verden.
- Rusin, Dave: The Mathematical Atlas, http://www.math-atlas.org Arkiveret 3. april 2004 hos Wayback Machine. En tur gennem de forskellige grene i moderne matematik.
- Weisstein, Eric: World of Mathematics, http://www.mathworld.com. En online encyklopædi om matematik.
- Planet Math, http://planetmath.org. En online encyklopædi om matematik under konstruktion. Bruger GNU Free Documentation License, så det tillader importering til Wikipedia. Bruger TeX markup.
- Mathematical Society of Japan: Encyclopedic Dictionary of Mathematics, 2nd ed. MIT Press, Cambridge, Mass., 1993. Definitioner, teoremer og referencer.
- Michiel Hazewinkel (ed.): Encyclopaedia of Mathematics. Kluwer Academic Publishers 2000. En oversat og udvidet version af den sovjetiske matematik encyklopædi, i ti (store) bøger, det mest komplette og autoritative værk der er tilgængeligt. Også som paperback og på CD-ROM.
- Gullberg, Jan: Mathematics—From the Birth of Numbers. W.W. Norton, 1996. Et encyklopædisk overblik over matematikken i et nutidigt og simpelt sprog
- Aigner, Martin; Ziegler, Günter (2009). Proofs from THE BOOK (4. udgave). Berlin, New York: Springer-Verlag. ISBN 978-3-642-00855-9.
- Kline, Morris (1990). Mathematical Thought from Ancient to Modern Times (Paperback udgave). New York: Oxford University Press. ISBN 978-0-19-506135-2.
- Oakley, Barbara (2014). A Mind For Numbers: How to Excel at Math and Science (Even If You Flunked Algebra). New York: Penguin Random House. ISBN 978-0-399-16524-5.
A Mind for Numbers.
Dansk
[redigér | rediger kildetekst]- Aksel Bertelsen (2010). Når matematikken slår rødder. Systime. ISBN 978-87-616-2628-8.
- Torben Braüner: Logikkens Muligheder og Grænser. Aktuel Naturvidenskab, 6, 2006.
- Jesper Frandsen (1992). Komplekse tal og fraktaler (1. udgave). Systime. ISBN 87-7783-188-8.
- Tinne Hoff Kjeldsen (2011). Hvad er matematik (1. udgave). Akademisk Forlag. ISBN 9788750041047.
- Mickaël Launay (2018). Den store fortælling om matematikken - fra forhistorisk tid til i dag. FADL's Forlag (oversat fra fransk). ISBN 978-87-93590-03-8.
- Henrik Kragh Sørensen (2017). Tal, Tænkepauser nr 47. Aarhus Universitet. ISBN 978-87-7124-502-8.
Lærebøger
[redigér | rediger kildetekst]- Erik Kristensen og Ole Rindung (1976): Matematik 1, G.E.C. Gads Forlag, 6. udgave, 260 sider, ISBN 87-12-47782-6.
- Claus Jessen, Peter Møller og Flemming Mørk (1999): Vektorregning og integralregning, gymnasiematematik niveau 3H, Gyldendal Uddannelse, 298 sider, ISBN 87-00-36966-7
- Morten Brydensholt og Grete Ridder Ebbesen (2010): Lærebog i matematik A1STX, Systime, 312 sider, ISBN 978-87-616-9454-6.
- Morten Brydensholt og Grete Ridder Ebbesen (2011): Lærebog i matematik A2STX, Systime, 356 sider, ISBN 978-87-616-9232-0.
- Morten Brydensholt og Grete Ridder Ebbesen (2019): Lærebog i matematik A3STX, Systime, 250 sider, ISBN 978-87-616-9356-3.
Formelsamlinger
[redigér | rediger kildetekst]- Bjarne Chr. Jensen (red., 2015): Teknisk Ståbi, kap. 1 Matematik, 23. udgave, Praxis, Nyt Teknisk Forlag, s. 19-54, ISBN 978-87-571-2844-4.
Noter
[redigér | rediger kildetekst]- ^ Her forstås algebra i dens moderne betydning, som er, groft sagt, kunsten at manipulere formler.
- ^ Generelt gælder for vilkårlige heltal , og , at hvis og , så
- ^ Kan huskes på, den store stikker til den lille, fx 7 > 5 og 5 < 7.
- ^ Her kræves normalt, sætningen skal være bevist ved to af hinanden uafhængige beregninger, med hver sin software.
Referencer
[redigér | rediger kildetekst]- ^ a b "mathematics, n.". Oxford English Dictionary. Oxford University Press. 2012. Arkiveret fra originalen 16. november 2019. Hentet 16. juni 2012.
The science of space, number, quantity, and arrangement, whose methods involve logical reasoning and usually the use of symbolic notation, and which includes geometry, arithmetic, algebra, and analysis.
- ^ Kneebone, G.T. (1963). Mathematical Logic and the Foundations of Mathematics: An Introductory Survey. Dover. s. 4. ISBN 978-0-486-41712-7. Arkiveret fra originalen 7. januar 2017. Hentet 20. juni 2015.
Mathematics ... is simply the study of abstract structures, or formal patterns of connectedness.
- ^ LaTorre, Donald R.; Kenelly, John W.; Biggers, Sherry S.; Carpenter, Laurel R.; Reed, Iris B.; Harris, Cynthia R. (2011). Calculus Concepts: An Informal Approach to the Mathematics of Change. Cengage Learning. s. 2. ISBN 978-1-4390-4957-0. Arkiveret fra originalen 7. januar 2017. Hentet 20. juni 2015.
Calculus is the study of change—how things change, and how quickly they change.
- ^ Ramana, B. V. (2007). Applied Mathematics. Tata McGraw–Hill Education. s. 2.10. ISBN 978-0-07-066753-2. Arkiveret fra originalen 12. juli 2022. Hentet 30. juli 2022.
The mathematical study of change, motion, growth or decay is calculus.
- ^ Ziegler, Günter M. (2011). "What Is Mathematics?". An Invitation to Mathematics: From Competitions to Research. Springer. s. vii. ISBN 978-3-642-19532-7. Arkiveret fra originalen 7. januar 2017. Hentet 20. juni 2015.
- ^ Wise, David. "Eudoxus' Influence on Euclid's Elements with a close look at The Method of Exhaustion". jwilson.coe.uga.edu. Arkiveret fra originalen 1. juni 2019. Hentet 26. oktober 2019.
- ^ Kjeldsen (2011), s. 10
- ^ Lothar Schmidt !980): Aphorismen von A–Z. Das große Handbuch geflügelter Definitionen. Drei Lilien Verlag, Wiesbaden, s. 288–289
- ^ Johannes Møllehave (1985): H.C. Andersens salt – Om humoren i H.C. Andersens eventyr. Lindhardt og Ringhof,Gyldendals Tranebøger, 265 sider, ISBN 87-7560-997-5, s. 87
- ^ a b c Mura, Roberta (december 1993). "Images of Mathematics Held by University Teachers of Mathematical Sciences". Educational Studies in Mathematics. 25 (4): 375-85. doi:10.1007/BF01273907. ISSN 0013-1954. JSTOR 3482762.
- ^ a b Tobies, Renate & Helmut Neunzert (2012). Iris Runge: A Life at the Crossroads of Mathematics, Science, and Industry. Springer. s. 9. ISBN 978-3-0348-0229-1.
[I]t is first necessary to ask what is meant by mathematics in general. Illustrious scholars have debated this matter until they were blue in the face, and yet no consensus has been reached about whether mathematics is a natural science, a branch of the humanities, or an art form.
- ^ Franklin, James (2009-07-08). Philosophy of Mathematics. s. 104. ISBN 978-0-08-093058-9. Arkiveret fra originalen 6. september 2015. Hentet 20. juni 2015.
- ^ Cajori, Florian (1893). A History of Mathematics. American Mathematical Society (1991 reprint). s. 285–86. ISBN 978-0-8218-2102-2.
- ^ Snapper, Ernst (september 1979). "The Three Crises in Mathematics: Logicism, Intuitionism, and Formalism". Mathematics Magazine. 52 (4): 207-16. Bibcode:1975MathM..48...12G. doi:10.2307/2689412. JSTOR 2689412.
- ^ Brezina, Corona (2006), Al-Khwarizmi: The Inventor of Algebra, The Rosen Publishing Group, s. 39-40, ISBN 978-1-4042-0513-0
- ^ Kjeldsen (2011), s. 34
- ^ Kjeldsen (2011), s. 39
- ^ Kjeldsen (2011), s. 43, 92
- ^ Kjeldsen (2011), s. 11, 58
- ^ Kjeldsen (2011), s. 68
- ^ Meinhard E. Mayer (2001). "The Feynman Integral and Feynman's Operational Calculus". Physics Today. 54 (8): 48. Bibcode:2001PhT....54h..48J. doi:10.1063/1.1404851.
- ^ Wigner, Eugene (1960). "The Unreasonable Effectiveness of Mathematics in the Natural Sciences". Communications on Pure and Applied Mathematics. 13 (1): 1-14. Bibcode:1960CPAM...13....1W. doi:10.1002/cpa.3160130102. Arkiveret fra originalen 28. februar 2011.
- ^ "Mathematics Subject Classification 2010" (PDF). Arkiveret (PDF) fra originalen 14. maj 2011. Hentet 9. november 2010.
- ^ James Williamson (translator and commentator), The Elements of Euclid, With Dissertations, Clarendon Press, Oxford, 1782, page 63.
- ^ Ore, Oystein (1988) [1948], Number Theory and its History, Dover, s. 65
- ^ Hardy, G. H. (1940). A Mathematician's Apology. Cambridge University Press. ISBN 978-0-521-42706-7.
- ^ Aigner & Ziegler (2009).
- ^ Gold, Bonnie; Simons, Rogers A. (2008). Proof and Other Dilemmas: Mathematics and Philosophy. MAA.
- ^ "Earliest Uses of Various Mathematical Symbols". Arkiveret fra originalen 20. februar 2016. Hentet 14. september 2014.
- ^ Kline (1980), p. 140, om Diofant; p. 261, om François Viète.
- ^ Oakley 2014, p. 16: "Focused problem solving in math and science is often more effortful than focused-mode thinking involving language and people. This may be because humans haven't evolved over the millennia to manipulate mathematical ideas, which are frequently more abstractly encrypted than those of conventional language."
- ^ Oakley 2014, p. 16: "What do I mean by abstractness? You can point to a real live cow chewing its cud in a pasture and equate it with the letters c–o–w on the page. But you can't point to a real live plus sign that the symbol '+' is modeled after – the idea underlying the plus sign is more abstract."
- ^ Oakley 2014, p. 16: "By encryptedness, I mean that one symbol can stand for a number of different operations or ideas, just as the multiplication sign symbolizes repeated addition."
- ^ Kjeldsen (2011), s. 37-38
- ^ Ivars Peterson, The Mathematical Tourist, Freeman, 1988, ISBN 0-7167-1953-3. p. 4 "A few complain that the computer program can't be verified properly", (in reference to the Haken–Apple proof of the Four Color Theorem).
- ^ matematik | lex.dk – Den Store Danske
- ^ Luke Howard Hodgkin & Luke Hodgkin, A History of Mathematics, Oxford University Press, 2005.
- ^ "The method of 'postulating' what we want has many advantages; they are the same as the advantages of theft over honest toil." Bertrand Russell (1919), Introduction to Mathematical Philosophy, New York and London, p. 71. Arkiveret 20. juni 2015 hos Wayback Machine
- ^ Patrick Suppes, Axiomatic Set Theory, Dover, 1972, ISBN 0-486-61630-4. p. 1, "Among the many branches of modern mathematics set theory occupies a unique place: with a few rare exceptions the entities which are studied and analyzed in mathematics may be regarded as certain particular sets or classes of objects."
- ^ Brydensholt & Ridder Ebbesen (2011), s. 154-160.
- ^ Brydensholt & Ridder Ebbesen (2011), s. 161-163.
- ^ Brydensholt & Ridder Ebbesen (2011), s. 171-176.
- ^ Brydensholt & Ridder Ebbesen (2011), s. 187-192.
- ^ Brydensholt & Ridder Ebbesen (2010), s. 16.
- ^ "number, n." OED Online (britisk engelsk). Oxford University Press. Arkiveret fra originalen 2018-10-04. Hentet 2017-05-16.
- ^ Matson, John. "The Origin of Zero". Scientific American (engelsk). Arkiveret fra originalen 2017-08-26. Hentet 2017-05-16.
- ^ a b Hodgkin, Luke (2005-06-02). A History of Mathematics: From Mesopotamia to Modernity (engelsk). OUP Oxford. s. 85-88. ISBN 978-0-19-152383-0. Arkiveret fra originalen 2019-02-04. Hentet 2017-05-16.
- ^ T.K. Puttaswamy, "The Accomplishments of Ancient Indian Mathematicians", pp. 410–11. In: Selin, Helaine; D'Ambrosio, Ubiratan, red. (2000), Mathematics Across Cultures: The History of Non-western Mathematics, Springer, ISBN 1-4020-0260-2.
- ^ a b Descartes, René (1954) [1637], La Géométrie | The Geometry of René Descartes with a facsimile of the first edition, Dover Publications, ISBN 0-486-60068-8, hentet 20. april 2011
- ^ Erik Lund, Mogens Pihl og Johannes Sløk (1962): De europæiske ideers historie. Gyldendal, 375 sider, s. 52
- ^ Plato, Theaetetus, p. 147 B, (for example, Jowett 1871), cited in von Fritz 2004, s. 212: "Theodorus was writing out for us something about roots, such as the roots of three or five, showing that they are incommensurable by the unit;..." See also Spiral of Theodorus.
- ^ von Fritz 2004.
- ^ H.E. Slaught and N.J. Lennes, Elementary algebra, Publ. Allyn and Bacon, 1915, page 1 (republished by Forgotten Books)
- ^ Lewis Hirsch, Arthur Goodman, Understanding Elementary Algebra With Geometry: A Course for College Students, Publisher: Cengage Learning, 2005, ISBN 0534999727, 9780534999728, 654 pages, page 2
- ^ Dividing by zero, på mathisfun.com
- ^ Sin Kwai Meng, Chip Wai Lung, Ng Song Beng, "Algebraic notation", in Mathematics Matters Secondary 1 Express Textbook, Publisher Panpac Education Pte Ltd, ISBN 9812738827, 9789812738820, page 68
- ^ "Arkiveret kopi". Arkiveret fra originalen 20. februar 2021. Hentet 22. august 2020.
- ^ Richard N. Aufmann, Joanne Lockwood, Introductory Algebra: An Applied Approach, Publisher Cengage Learning, 2010, ISBN 1439046042, 9781439046043, page 78
- ^ William L. Hosch (editor), The Britannica Guide to Algebra and Trigonometry, Britannica Educational Publishing, The Rosen Publishing Group, 2010, ISBN 1615302190, 9781615302192, page 71
- ^ James E. Gentle, Numerical Linear Algebra for Applications in Statistics, Publisher: Springer, 1998, ISBN 0387985425, 9780387985428, 221 pages, [James E. Gentle page 183]
- ^ Horatio Nelson Robinson, New elementary algebra: containing the rudiments of science for schools and academies, Ivison, Phinney, Blakeman, & Co., 1866, page 7
- ^ Ron Larson, Robert Hostetler, Bruce H. Edwards, Algebra And Trigonometry: A Graphing Approach, Publisher: Cengage Learning, 2007, ISBN 061885195X, 9780618851959, 1114 pages, page 6
- ^ David Alan Herzog, Teach Yourself Visually Algebra, Publisher John Wiley & Sons, 2008, ISBN 0470185597, 9780470185599, 304 pages, page 72
- ^ John C. Peterson, Technical Mathematics With Calculus, Publisher Cengage Learning, 2003, ISBN 0766861899, 9780766861893, 1613 pages, page 31
- ^ Jerome E. Kaufmann, Karen L. Schwitters, Algebra for College Students, Publisher Cengage Learning, 2010, ISBN 0538733543, 9780538733540, 803 pages, page 222
- ^ Thomas Sonnabend, Mathematics for Teachers: An Interactive Approach for Grades K-8, Publisher: Cengage Learning, 2009, ISBN 0495561665, 9780495561668, 759 pages, page xvii
- ^ Lewis Hirsch, Arthur Goodman, Understanding Elementary Algebra With Geometry: A Course for College Students, Publisher: Cengage Learning, 2005, ISBN 0534999727, 9780534999728, 654 pages, page 48
- ^ Lawrence S. Leff, College Algebra: Barron's Ez-101 Study Keys, Publisher: Barron's Educational Series, 2005, ISBN 0764129147, 9780764129148, 230 pages, page 2
- ^ Ron Larson, Kimberly Nolting, Elementary Algebra, Publisher: Cengage Learning, 2009, ISBN 0547102275, 9780547102276, 622 pages, page 210
- ^ Charles P. McKeague, Elementary Algebra, Publisher: Cengage Learning, 2011, ISBN 0840064217, 9780840064219, 571 pages, page 49
- ^ a b Helmuth Gericke (1994). Talbegrebets historie. Oversat af Kirsti Andersen og Kate Larsen. Matematiklærerforeningen, Aarhus Universitet. ISBN 87-89229-66-5.
- ^ Jens Carstensen. Komplekse tal. Systime, 3. udgave 1995. ISBN 87 7783 412 7.
- ^ Frandsen (1992), s. 9.
- ^ Frandsen (1992), s. 10.
- ^ Christian Berg (2004). "Kompleks funktionsteori", Noter. Københavns Universitet, Matematisk Afdeling.
- ^ René Descartes (1954) [1637]. La Géométrie | The Geometry of René Descartes with a facsimile of the first edition. Dover Publications. ISBN 978-0-486-60068-0. Hentet 20. april 2011.
- ^ Frandsen (1992), s. 19.
- ^ Frandsen (1992), s. 16-25.
- ^ Frandsen (1992), s. 41.
- ^ Brydensholt & Ridder Ebbesen (2011), s. 217.
- ^ History of Vectors, McGill
- ^ Brydensholt & Ridder Ebbesen (2011), s. 220-226.
- ^ a b c d Birger Iversen: algebra, i Den Store Danske på lex.dk. Hentet 23. august 2020
- ^ Kjeldsen (2011), s. 116-118
- ^ Tapson, Frank (1996). The Oxford Mathematics Study Dictionary. Oxford University Press. ISBN 0-19-914551-2.
- ^ Launay (2018), s. 52.
- ^ Vincenzo De Risi (31. januar 2015). Mathematizing Space: The Objects of Geometry from Antiquity to the Early Modern Age. Birkhäuser. s. 1–. ISBN 978-3-319-12102-4.
- ^ Tabak, John (2014). Geometry: the language of space and form. Infobase Publishing. s. xiv. ISBN 978-0816049530.
- ^ Launay (2018), s. 72-73.
- ^ Bertelsen (2010), s. 18.
- ^ Launay (2018), s. 241.
- ^ Launay (2018), s. 103-104.
- ^ Boris A. Rosenfeld & Adolf P. Youschkevitch, "Geometry", p. 470, in Roshdi Rashed & Régis Morelon (1996), Encyclopedia of the History of Arabic Science, Vol. 2, pp. 447–494, Routledge, London and New York:
"Three scientists, Ibn al-Haytham, Khayyam, and al-Tusi, had made the most considerable contribution to this branch of geometry, whose importance was completely recognized only in the nineteenth century. In essence, their propositions concerning the properties of quadrangle—which they considered assuming that some of the angles of these figures were acute of obtuse—embodied the first few theorems of the hyperbolic and the elliptic geometries. Their other proposals showed that various geometric statements were equivalent to the Euclidean postulate V. It is extremely important that these scholars established the mutual connection between this postulate and the sum of the angles of a triangle and a quadrangle. By their works on the theory of parallel lines Arab mathematicians directly influenced the relevant investigations of their European counterparts. The first European attempt to prove the postulate on parallel lines – made by Witelo, the Polish scientists of the thirteenth century, while revising Ibn al-Haytham's Book of Optics (Kitab al-Manazir) – was undoubtedly prompted by Arabic sources. The proofs put forward in the fourteenth century by the Jewish scholar Levi ben Gerson, who lived in southern France, and by the above-mentioned Alfonso from Spain directly border on Ibn al-Haytham's demonstration. Above, we have demonstrated that Pseudo-Tusi's Exposition of Euclid had stimulated borth J. Wallis's and G. Saccheri's studies of the theory of parallel lines."
- ^ Felix Klein, Elementary Mathematics from an Advanced Standpoint: Geometry, Dover, 1948 (reprint of English translation of 3rd Edition, 1940. First edition in German, 1908) pg. 176
- ^ Ikke-euklidisk geometri, artikel i Raunkjærs Konversationsleksikon, bd. 6, sp. 46-47, Det danske Forlag, København 1950
- ^ Frandsen (1992), s. 62-64.
- ^ Frandsen (1992), s. 58.
- ^ Frandsen (1992), s. 103.
- ^ Frandsen (1992), s. 110.
- ^ Frandsen (1992), s. 128-130.
- ^ Launay (2018), s. 250-251.
- ^ Launay (2018), s. 264-265.
- ^ differentialregning, artikel af Jesper Lützen i denstoredanske
- ^ Brydensholt & Ridder Ebbesen (2010), s. 145-147.
- ^ Brydensholt & Ridder Ebbesen (2010), s. 151-155.
- ^ "Compendium of Mathematical Symbols". Math Vault (amerikansk engelsk). 2020-03-01. Hentet 2020-08-28.
- ^ Brydensholt & Ridder Ebbesen (2011), s. 108.
- ^ Brydensholt & Ridder Ebbesen (2011), s. 39.
- ^ Brydensholt & Ridder Ebbesen (2011), s. 39,47.
- ^ Brydensholt & Ridder Ebbesen (2011), s. 42.
- ^ Brydensholt & Ridder Ebbesen (2011), s. 40,60.
- ^ Brydensholt & Ridder Ebbesen (2011), s. 49-59.
- ^ http://olewitthansen.dk/Matematik/Differentialregning.pdf
- ^ Differentialregning
- ^ Brydensholt & Ridder Ebbesen (2011), s. 97-111.
- ^ Jessen m.fl. (1999), s. 136.
- ^ Jessen m.fl. (1999), s. 136-140.
- ^ Jessen m.fl. (1999), s. 172-173.
- ^ Jessen m.fl. (1999), s. 168.
- ^ Jessen m.fl. (1999), s. 139,165.
- ^ Jessen m.fl. (1999), s. 176.
- ^ Jessen m.fl. (1999), s. 178.
- ^ Jessen m.fl. (1999), s. 200.
- ^ differentialligning, artikel på lex.dk af Gerd Grubb
- ^ Jessen m.fl. (1999), s. 226-229.
- ^ Jessen m.fl. (1999), s. 215-216.
- ^ David Wells (1988). "Which is the most beautiful?". Mathematical Intelligencer. 10 (4): 30-31. .
- ^ David Wells (1990). "Are these the most beautiful?". Mathematical Intelligencer. 12(3): 37-41. .
- ^ Heinz Duthel (2018): Discover Entdecke Découvrir Astronomie - Apokalypse Der Weg in die Geheimnisse des Anfangs und des Ende: Einleitung in astronomische Beobachtungen. Grundlagenwissen über Teleskope und dessen Bedienung. 648 sider ISBN 9783742734655
Eksterne henvisninger
[redigér | rediger kildetekst] |
Wikimedia Commons har medier relateret til: |
Opgaver
[redigér | rediger kildetekst]Ordbøger
[redigér | rediger kildetekst]Generel
[redigér | rediger kildetekst]- Wolfram: Eric Weisstein's World of Mathematics
- Citater om matematik
- Mathematische Kleinigkeiten (forældet side?)
- The Prime Pages Arkiveret 1. august 2003 hos Wayback Machine
- MathPuzzle.com
Historie
[redigér | rediger kildetekst]- Egyptian Mathematics Arkiveret 13. oktober 2004 hos Wayback Machine
- Noter til: Whitehead og Russell (1910-12): Principia Mathematica
- Jørgen Ebert (1995): Komplekse tal - en historisk og aksiomatisk introduktion. Forlaget Minor































































![{\displaystyle x={\sqrt[{3}]{q/2+{\sqrt {(q/2)^{2}-(p/3)^{3}}}}}+{\sqrt[{3}]{q/2-{\sqrt {(q/2)^{2}-(p/3)^{3}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4093f1a94136fbe89eca11f15c2ab50729537f0)


![{\displaystyle x={\sqrt[{3}]{2+{\sqrt {-121}}}}+{\sqrt[{3}]{2-{\sqrt {-121}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/573262f780972f7c7b785df859855e4894ca6709)





![{\displaystyle x={\sqrt[{3}]{2+{\sqrt {-121}}}}+{\sqrt[{3}]{2-{\sqrt {-121}}}}=2+{\sqrt {-1}}+2-{\sqrt {-1}}=4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbc66f5202d65646513b1f7a6756bfde9588ccab)










![{\displaystyle {\vec {a}}=[a_{1},a_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bddd5cae712e5e702d68abffa398ca6c1c9827ba)












































































































![{\displaystyle [1,2,3][1,3,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3456de48f67f15147542c745a3a8cbe64d9ed7e)
![{\displaystyle [2,1,3][2,3,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2982b802b037da0f46b428d63581818291e5a8bd)
![{\displaystyle [3,1,2][3,2,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fd3d1378424e83c7f56eef8db2ea044b149c25a)